题目内容

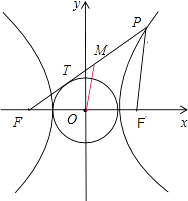
【题目】从双曲线 ﹣ =1（a＞0，b＞0）的左焦点F引圆x2+y2=a2的切线，切点为T，延长FT交双曲线右支于P点，若M为线段FP的中点，O为坐标原点，则|MO|﹣|MT|等于（ ）
A.c﹣a
B.b﹣a
C.a﹣b
D.c﹣b

【答案】B
【解析】解：如图所示，设F′是双曲线的右焦点，连接PF′．

∵点M，O分别为线段PF，FF′的中点，

由三角形中位线定理得到：|OM|= |PF′|= （|PF|﹣2a）= |PF|﹣a

=|MF|﹣a，

∴|OM|﹣|MT|=|MF|﹣|MT|﹣a=|FT|﹣a，连接OT，因为PT是圆的切线，

则OT⊥FT，

在Rt△FOT中，|OF|=c，|OT|=a，

∴|FT|= =b．

∴|OM|﹣|MT|=b﹣a．

故选B．

练习册系列答案
相关题目

【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD为菱形，E为AC与BD的交点，PA⊥平面ABCD，M为PA中点，N为BC中点．
（1）证明：直线MN∥平面PCD；
（2）若点Q为PC中点，∠BAD=120°，PA= ，AB=1，求三棱锥A﹣QCD的体积．

【题目】如图，在棱台ABC﹣FED中，△DEF与△ABC分别是棱长为1与2的正三角形，平面ABC⊥平面BCDE，四边形BCDE为直角梯形，BC⊥CD，CD=1，N为CE中点， ．
（1）λ为何值时，MN∥平面ABC？
（2）在（1）的条件下，求直线AN与平面BMN所成角的正弦值．

【题目】设A是双曲线 的右顶点，F（c，0）是右焦点，若抛物线 的准线l上存在一点P，使∠APF=30°，则双曲线的离心率的范围是（ ）
A.[2，+∞）
B.（1，2]
C.（1，3]
D.[3，+∞）

【题目】已知函数f（x）=2xlnx﹣x2+2ax，其中a＞0．
（1）设g（x）是f（x）的导函数，求函数g（x）的极值；
（2）是否存在常数a，使得x∈[1，+∞）时，f（x）≤0恒成立，且f（x）=0有唯一解，若存在，求出a的值；若不存在，说明理由．

【题目】已知椭圆C1的方程为 + =1，双曲线C2的左、右焦点分别是C1的左、右顶点，而以双曲线C2的左、右顶点分别是椭圆C1的左、右焦点．
（1）求双曲线C2的方程；
（2）记O为坐标原点，过点Q（0，2）的直线l与双曲线C2相交于不同的两点E、F，若△OEF的面积为2 ，求直线l的方程．

【题目】甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2、3、4，乙袋中红色、黑色、白色小球的个数均为3，某人用左手从甲袋中取球，用右手从乙袋中取球，
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若一次在同一袋中取出两球，如果两球颜色相同则称这次取球获得成功．某人第一次左手先取两球，第二次右手再取两球，记两次取球的获得成功的次数为随机变量X，求X的分布列和数学期望．

【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表：

使用年数x（单位：年）

1

2

3

4

5

维修总费用y（单位：万元）

0.5

1.2

2.2

3.3

4.5

根据上表可得y关于x的线性回归方程 = x﹣0.69，若该汽车维修总费用超过10万元就不再维修，直接报废，据此模型预测该汽车最多可使用（ ）
A.8年
B.9年
C.10年
D.11年

【题目】已知函数f（x）= ，若f（x）的两个零点分别为x1 ， x2 ， 则|x1﹣x2|=（ ）
A.
B.1+
C.2
D. +ln2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网