题目内容
15．设x＞0，y＞0，向量$\overrightarrow a$=（1-x，4），$\overrightarrow b$=（x，-y），若$\overrightarrow a$∥$\overrightarrow b$，则x+y的最小值为9．分析 先根据向量平行得到$\frac{1}{x}$+$\frac{4}{y}$=1，再利用基本不等式即可求出最值．
解答 解：因为$\overrightarrow a$∥$\overrightarrow b$，
所以4x+（1-x）y=0，
又x＞0，y＞0，
所以$\frac{1}{x}$+$\frac{4}{y}$=1，
故x+y=（$\frac{1}{x}$+$\frac{4}{y}$）（x+y）=5+$\frac{y}{x}$+$\frac{4x}{y}$≥9．
当$\frac{y}{x}$=$\frac{4x}{y}$，$\frac{1}{x}$+$\frac{4}{y}$=1同时成立，即x=3，y=6时，等号成立．
（x+y）min=9．
故答案为：9．
点评 本题考查了向量平行的条件和基本不等式的应用，属于基础题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
如图，在△ABC中，BC边上的中线为AD．
3．如图所示的流程图，现输入以下函数，则可以输出的函数是（ ）
| A． | f（x）=sinx | B． | f（x）=|x| | C． | f（x）=$\frac{1}{2}$（2x+2-x） | D． | f（x）=ln$\frac{2-x}{2+x}$ |
对一批产品的长度（单位：毫米）进行抽样检测，样本容量为400，右图为检测结果的频率分布直方图，根据产品标准，单件产品长度在区间[25，30）的为一等品，在区间[20，25）和[30，35）的为二等品，其余均为三等品，则样本中三等品的件数为100．
4．若某几何体的三视图如图所示，则此几何体的体积是（ ）
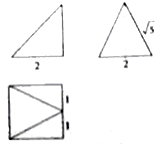
| A． | 4$\sqrt{5}$ | B． | $\frac{4\sqrt{5}}{3}$ | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
5．已知集合A={0，1，2，3，4}，集合B={y|y=$\sqrt{x}$，x∈A}．则集合A∩B=（ ）
| A． | {0} | B． | {0，1} | C． | {0，1，2} | D． | {0，1，2，4} |