题目内容
3.如图所示的流程图,现输入以下函数,则可以输出的函数是( )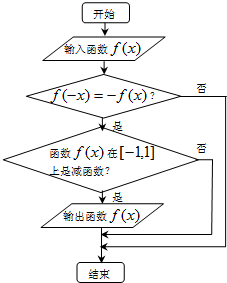
| A. | f(x)=sinx | B. | f(x)=|x| | C. | f(x)=$\frac{1}{2}$(2x+2-x) | D. | f(x)=ln$\frac{2-x}{2+x}$ |
分析 本题的框图是一个选择结构,其算法是找出即是奇函数且在[-1,1]上为减函数的函数,由此规则对四个选项进行比对,即可得出正确选项.
解答 解:解:由框图可判断出框图的功能是输出的函数f(x)既是奇函数又在[-1,1]上为减函数,
A中,f(x)=sinx为奇函数,但在[-1,1]上为增函数;
B中,f(x)=|x|为偶函数,
C中,f(x)=$\frac{1}{2}$(2x+2-x)为偶函数,
D中,f(x)=ln$\frac{2-x}{2+x}$既是奇函数又在[-1,1]上为减函数,
故选:D
点评 本题考查的知识点是程序框图和函数的图象与性质,根据程序框图的流程能够判断出框图的功能是解答的关键.

练习册系列答案
相关题目
14.在如图所示的茎叶图中,若甲组数据众数为14,则乙组数据的中位数为( )
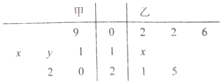

| A. | 6 | B. | 8 | C. | 10 | D. | 14 |
11.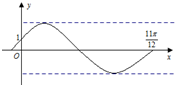 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )| A. | ω=$\frac{10}{11}$,φ=$\frac{π}{6}$ | B. | ω=2,φ=$\frac{π}{12}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=$\frac{10}{11}$,φ=$\frac{π}{12}$ |
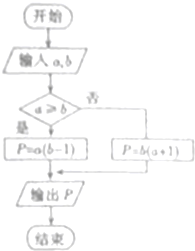 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )