题目内容
5.已知集合A={0,1,2,3,4},集合B={y|y=$\sqrt{x}$,x∈A}.则集合A∩B=( )| A. | {0} | B. | {0,1} | C. | {0,1,2} | D. | {0,1,2,4} |
分析 把A中的元素代入B中求出y的值,确定出B,找出A与B的交集即可.
解答 解:把x=0,1,2,3,4分别代入y=$\sqrt{x}$,得:y=0,1,$\sqrt{2}$,$\sqrt{3}$,2,即B={0,1,$\sqrt{2}$,$\sqrt{3}$,2},
∵A={0,1,2,3,4},
∴A∩B={0,1,2},
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
16.若复数z=a+bi(i为虚数单位,a,b∈R)在复平面内对应点为Z(a,b),O为坐标原点,将实轴非负半轴绕点O逆时针旋转到OZ,转过的最小角叫复数z的辐角主值,记作arg(z),则arg($\frac{2}{1-i}$)的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
10.计算$\frac{2i}{1-i}$(i为虚数单位)等于( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
17.如图,$\overrightarrow{OC}=2\overrightarrow{OP}$,$\overrightarrow{AB}=2\overrightarrow{AC}$,$\overrightarrow{OM}=m\overrightarrow{OB}$,$\overrightarrow{ON}=n\overrightarrow{OA}$,若m=$\frac{3}{8}$,那么n=( )
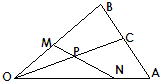

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
14.已知命题p:?x∈R,x2-2x-4≤0,则¬p为( )
| A. | ?x∈R,x2-2x-4≥0 | B. | ?x0∈R,x02-2x0-4>0 | ||
| C. | ?x∉R,x2-2x+4≤0 | D. | ?x0∈R,x02-2x0-4>0 |
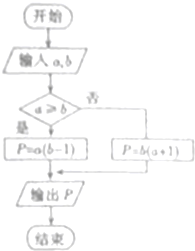 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )