题目内容
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了
个进行测量,根据所测量的数据画出频率分布直方图如下:
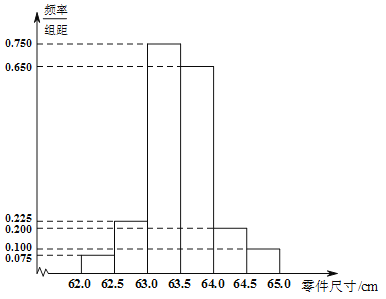
注:尺寸数据在
内的零件为合格品,频率作为概率.
(Ⅰ) 从产品中随机抽取
件,合格品的个数为
,求的分布列与期望；
(Ⅱ) 从产品中随机抽取
件,全是合格品的概率不小于
,求的最大值；
(Ⅲ) 为了提高产品合格率,现提出
两种不同的改进方案进行试验.若按
方案进行试验后,随机抽取
件产品,不合格个数的期望是
；若按
方案试验后,抽取
件产品,不合格个数的期望是,你会选择哪个改进方案?
【答案】(Ⅰ)分布列见解析，
； (Ⅱ)
； (Ⅲ)选择方案
.
【解析】
(Ⅰ)先根据直方图求出合格率，然后求出ξ的可能取值和相应的概率，作分布列，再利用随机变量的分布列进行求期望；
(Ⅱ)根据n件产品都合格的概率大于等于0.3，列不等式求解n的最大值；
(Ⅲ)根据期望求出A，B方案不合格的概率，即可选择.
(Ⅰ)由直方图可知,抽出产品为合格品的频率为
,即抽出产品为合格品的概率为
, 从产品中随机抽取
件,合格品的个数
的所有可能取值为
且 
,
,
, 
,
, 所以的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
故数学期望
(Ⅱ) 随机抽取
件,全是合格品的概率为
,依题意
,故的最大值为.
(Ⅲ) 按方案随机抽取产品不合格的概率是
,随机抽取
件产品,不合格个数
；
按
方案随机抽取产品不合格的概率是
,随机抽取
件产品,不合格个数
,
依题意
,
,解得
,
因为
,所以应选择方案.
新题型全程检测期末冲刺100分系列答案
【题目】某次考试中500名学生的物理（满分为150分）成绩服从正态分布
，数学成绩的频率分布直方图如图所示．
（Ⅰ）如果成绩大于135分为特别优秀，那么本次考试中的物理、数学特别优秀的大约各有多少人？
（Ⅱ）如果物理和数学两科都特别优秀的共有4人，是否有99.9%的把握认为物理特别优秀的学生，数学也特别优秀？
附：①若
，则
②表及公式：
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【题目】为推进“千村百镇计划”，2019年4月某新能源公司开展“电动绿色出行”活动，首批投放200台
型新能源车到某地多个村镇，供当地村民免费试用三个月.试用到期后，为了解男女试用者对型新能源车性能的评价情况，该公司要求每位试用者填写一份性能综合评分表（满分为100分）.最后该公司共收回有效评分表600份，现从中随机抽取40份（其中男、女的评分表各20份）作为样本，经统计得到茎叶图：
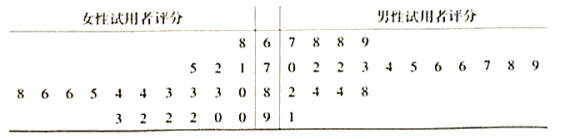
（1）求40个样本数据的中位数
；
（2）已知40个样本数据的平均数
，记与
的最大值为
.该公司规定样本中试用者的“认定类型”：评分不小于的为“满意型”，评分小于的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中，评分小于的份数；
②请根据40个样本数据，完成下面2×2列联表：
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关？
附：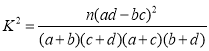
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
