题目内容
【题目】设n为给定的大于2的整数。有n个外表上没有区别的袋子,第k(k=1,2,···,n)个袋中有k个红球,n-k个白球。将这些袋子混合后,任选一个袋子,并且从中连续取出三个球(每次取出不放回)。求第三次取出的为白球的概率。
【答案】![]()
【解析】
设选出的是第k个袋子,连续三次取球的方法数为n(n-1)(n-2).
第三次取出的是白球的三次取球颜色有如下四种情形:
(白,白,白)取法数为 (n-k)(n-k-1)(n-k-2),
(白,红,白)取法数为k(n-k)(n-k-1),
(红,白,白)取法数为k(n-k)(n-k-1),
(红,红,白)取法数为k(k-1)(n-k).
从而,第三次取出的是白球的种数为
(n-k)(n-k-1)(n-k-2)+k(n-k)(n-k-1)+k(n-k)(n-k-1)+k(k-1)(n-k)
=(n-1)(n-2)(n-k).
则在第h个袋子中第三次取出的是白球的概率为![]()
而选到第k个袋子的概率为![]() ,故所求的概率为
,故所求的概率为
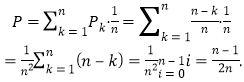

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某次考试中500名学生的物理(满分为150分)成绩服从正态分布![]() ,数学成绩的频率分布直方图如图所示.
,数学成绩的频率分布直方图如图所示.

(Ⅰ)如果成绩大于135分为特别优秀,那么本次考试中的物理、数学特别优秀的大约各有多少人?
(Ⅱ)如果物理和数学两科都特别优秀的共有4人,是否有99.9%的把握认为物理特别优秀的学生,数学也特别优秀?
附:①若![]() ,则
,则![]()
②表及公式:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |