题目内容
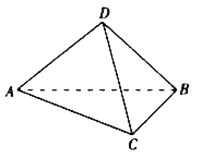
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() .已知
.已知![]() ,
,![]() 为线段
为线段![]() 上的一点,二面角
上的一点,二面角![]() 与二面角
与二面角![]() 的大小相等.则
的大小相等.则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
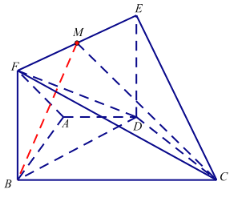
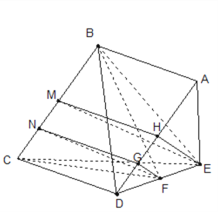
如图所示,过E作EH⊥AD于H,过H作MH⊥BC于M,连结ME,
同理过F作FG⊥AD于G,过G作NG⊥BC于N,连结NF,
AE⊥平面CDE,CD平面CDE,则AE⊥CD,CD⊥AD,
AE∩AD=A,AD,AE平面DAE,
CD⊥平面DAE,EH平面DAE,则CD⊥EH,
CD∩AD=D,CD,AD平面ABCD,EH⊥平面ABCD,
故HE⊥BC,BC⊥平面MHE,∠HME为二面角E-BC-D的平面角,
同理,∠GNF为二面角F-BC-D的平面角,
MH∥AB,![]() ,又
,又![]() ,
,
故tan∠HME=![]() ,而∠HME=2∠GNF,
,而∠HME=2∠GNF,
∴tan∠GNF=![]() ,
,![]() ,
,
又GF∥HE,![]() ,
,![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某次考试中500名学生的物理(满分为150分)成绩服从正态分布![]() ,数学成绩的频率分布直方图如图所示.
,数学成绩的频率分布直方图如图所示.

(Ⅰ)如果成绩大于135分为特别优秀,那么本次考试中的物理、数学特别优秀的大约各有多少人?
(Ⅱ)如果物理和数学两科都特别优秀的共有4人,是否有99.9%的把握认为物理特别优秀的学生,数学也特别优秀?
附:①若![]() ,则
,则![]()
②表及公式:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |