题目内容
已知Sn为正项数列{an}的前n项和，且满足Sn＝
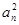＋an(n∈
N＋)，求出a1，a2，a3，a4，猜想{an}的通项公式并给出证明
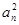＋an(n∈N＋)，求出a1，a2，a3，a4，猜想{an}的通项公式并给出证明
a1＝1，a2＝2，a3＝3，a4＝4，an＝n.
由Sn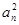＝＋an(n∈N＋)．
可得a1＝
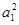＋a1，解得a1＝1，
S2＝a1＋a2＝
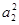＋a2，解得a2＝2，
同理a3＝3，a4＝4，猜想an＝n.
Sn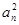＝＋an①
Sn－1＝
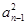＋an－1，(当n≥2时)②
①－②得(an－an－1－1)(an＋an－1)＝0，
∵an＋an－1≠0，∴an－an－1＝1，
又a1＝1，故数列{an}是首项a1＝1，公差d＝1的等差数列，
故an＝n.
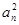＋an(n∈N＋)．可得a1＝
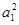＋a1，解得a1＝1，S2＝a1＋a2＝
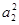＋a2，解得a2＝2，同理a3＝3，a4＝4，猜想an＝n.
Sn＝
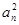＋an①Sn－1＝
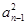＋an－1，(当n≥2时)②①－②得(an－an－1－1)(an＋an－1)＝0，
∵an＋an－1≠0，∴an－an－1＝1，
又a1＝1，故数列{an}是首项a1＝1，公差d＝1的等差数列，
故an＝n.
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
，分别求
，
，
，然后归纳猜想一般性结论
__________ ．
、
、
、
号位上（如图），第一次前后
这样交替进行下去，那么第
次互换座位后，小兔坐
…
…
，
的分解中最小的正整数是21，则
.
＝1的面积S＝πab
(n2－1)[1－(－1)n]的值 ( )
