题目内容
如图,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、
SC和底面ABC,所成的角分别为α1、α2、α3,三侧面SBC,SAC,SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间情形的一个猜想.

SC和底面ABC,所成的角分别为α1、α2、α3,三侧面SBC,SAC,SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间情形的一个猜想.

猜想 成立
成立
 成立
成立在△DEF中(如图),由正弦定理得 .
.
于是,类比三角形中的正弦定理,
在四面体S-ABC中,
我们猜想 成立.
成立.
 .
.于是,类比三角形中的正弦定理,
在四面体S-ABC中,
我们猜想
 成立.
成立.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
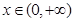 有下列各式:
有下列各式: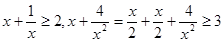 ,
,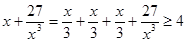 成立,观察上面各式,按此规律若
成立,观察上面各式,按此规律若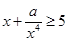 ,则正数
,则正数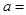 ( )
( )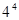
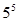
 ,f(2)=lg 15,则f(2 008)=________.
,f(2)=lg 15,则f(2 008)=________.
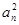 +
+ (x>0),观察f1(x)=f(x)=
(x>0),观察f1(x)=f(x)=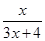 ,
, ,
, ,…
,…
 个正整数
个正整数 、
、 、
、 、…、
、…、 )任意排成
)任意排成 行
行 、
、 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当 时,数表的所有可能的“特征值”最大值为
时,数表的所有可能的“特征值”最大值为
