题目内容
20．在△ABC中，如果sinA=$\sqrt{3}$sinC，B=30°，那么角A=120°．分析 由题意和正弦定理可得a=$\sqrt{3}$c，再由余弦定理可得b2=c2，代入cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$化简可得余弦值，可角A
解答 解：∵sinA=$\sqrt{3}$sinC，
∴由正弦定理可得a=$\sqrt{3}$c，
又∵B=30°，
∴由余弦定理可得b2=a2+c2-2accosB，
代入数据可得b2=3c2+c2-3c2=c2，即b=c，
∴再由余弦定理可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$
=$\frac{{c}^{2}+{c}^{2}-3{c}^{2}}{2{c}^{2}}$=-$\frac{1}{2}$，∴A=120°
故答案为：120°．
点评 本题考查解三角形，涉及正余弦定理的综合应用，属中档题．
练习册系列答案
相关题目
11．铁矿石A和B的含铁率a，冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表：
某冶炼厂至少要生产1.9（万吨）铁，若要求CO2的排放量不超过2（万吨），求购买铁矿石的最少费用．
| a | b（万吨） | c（百万元） | |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
5．在一组样本数据（x1，y1），（x2，y2），…（xn，yn）（n≥2，x1，x2，…，xn不全相等）的散点图中，若所有样本点（xi，yi）（i=1，2，…，n）都在直线y=2x+1上，则这组样本数据的样本相关系数为（ ）
| A． | -1 | B． | 0 | C． | 2 | D． | 1 |
12．使cosx=1-m有意义的m的取值范围为（ ）
| A． | m≥0 | B． | 0≤m≤2 | C． | -1＜m＜1 | D． | m＜-1或m＞1 |
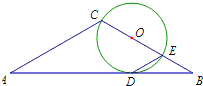如图，在△ACB中，∠ACB=120°，AC=BC=3，点O在BC边上，且圆O与AB相切于点D，BC与圆O相交于点E，C，则∠EDB=30°，BE=1．