��Ŀ����
����Ŀ��������ѧ���Ӽ��Ǹ�ϲ����������ˣ���ÿ�춼�Ṻ��һ����������ʦ�����Լ����۵�ÿ�������ƽ��������1000![]() �����¸���������50
�����¸���������50![]() .��仰����ѧ������������ǣ�ÿ�������������������Ϊ1000
.��仰����ѧ������������ǣ�ÿ�������������������Ϊ1000![]() ������Ϊ50
������Ϊ50![]() ����̬�ֲ�.
����̬�ֲ�.
��1���������ʦ��˵������ʵ�ģ������ʦ���۵��������ȡ��������ȡ���������������������1000![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��2����Ϊһ������˼������ѧ�ң��Ӽ���ÿ�춼�Ὣ������������ز���¼��25��õ��������±���������25�����������Ϊ24468![]() .�Ӽ��������25�����������ͳ�����ݣ���λ��
.�Ӽ��������25�����������ͳ�����ݣ���λ��![]() ��
��
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
�����������ݶ�����![]() �ϣ����ӼӲ˻�����Ϊ���ʦ���ѣ�����������Ϣ���Ӹ��ʽǶ�˵������
�ϣ����ӼӲ˻�����Ϊ���ʦ���ѣ�����������Ϣ���Ӹ��ʽǶ�˵������
����
����![]() ����X��ȡֵ�������ȡ25�����ݣ�����25�����ݵ�ƽ��ֵΪY������ͳ��ѧ֪ʶ��֪���������
����X��ȡֵ�������ȡ25�����ݣ�����25�����ݵ�ƽ��ֵΪY������ͳ��ѧ֪ʶ��֪���������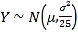
����![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��ͨ���ѷ���������0.05���µ��¼���ΪС�����¼�.
���𰸡���1���ֲ��м�����������Ϊ1��������2���������
��������
��1��������֪��![]() �����п���ȡֵΪ0��1��2.�����
�����п���ȡֵΪ0��1��2.�����![]() ��
��![]() ��
��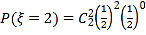 .�Ӷ������
.�Ӷ������![]() �ķֲ��к�����ѧ����.
�ķֲ��к�����ѧ����.
��2�������ʦ������ÿ�����������Ϊ�������X.�������ʦû�����ѣ���![]() .�ɸ��٣���X��ȡֵ�������ȡ25�����ݣ�����25�����ݵ�ƽ��ֵΪY����
.�ɸ��٣���X��ȡֵ�������ȡ25�����ݣ�����25�����ݵ�ƽ��ֵΪY����![]() .�������25�����ݵ�ƽ��ֵΪ
.�������25�����ݵ�ƽ��ֵΪ![]() �������ɸ�������֪��
�������ɸ�������֪��![]() ���ɸ���֪���¼���
���ɸ���֪���¼���![]() ��ΪС�����¼����ɵý���.
��ΪС�����¼����ɵý���.
��1��������֪��![]() �����п���ȡֵΪ0��1��2.
�����п���ȡֵΪ0��1��2.
![]() ��
��![]() ��
��
![]() .����
.����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 |
P |
|
|
|
����![]() ������.
������.
��2�������ʦ������ÿ�����������Ϊ�������X.
�������ʦû�����ѣ���![]() .
.
���ݸ�������X��ȡֵ�������ȡ25�����ݣ�����25�����ݵ�ƽ��ֵΪY��
��![]() .
.
�Ӽ�����¼��25������������൱�ڴ�X��ȡֵ�������ȡ��25�����ݣ�
��25�����ݵ�ƽ��ֵΪ![]() ��
��
�ɸ�������֪��![]() ��
��
�ɸ���֪���¼���![]() ��ΪС�����¼���
��ΪС�����¼���
�������������ʦû������������
�����Ӽ�����Ϊ���ʦ����.

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�