题目内容
11.对于任意的x1,x2∈R,且x1≠x2,若$f(x)={({\frac{1}{2}})^x},m=\frac{{f({x_1})+f({x_2})}}{2},n=f({\frac{{{x_1}+{x_2}}}{2}})$,则m与n的大小关系为m>n.分析 因为指数函数为下凸函数,借助于函数图象可得出答案.
解答  解:因为f(x)=($\frac{1}{2}$)x的图象是下凸函数,不妨设x1<x2
解:因为f(x)=($\frac{1}{2}$)x的图象是下凸函数,不妨设x1<x2
作出函数图象如图所示:易得m>n
故答案为m>n
点评 本题考查了指数函数的图象,指数函数图象是高考考查的重点内容之一,本题主要帮助学生掌握指数函数的下凸性.

练习册系列答案
相关题目
1.设F是双曲线$\frac{x^2}{4}$-$\frac{y^2}{12}$=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为( )
| A. | 5 | B. | 5+4$\sqrt{3}$ | C. | 7 | D. | 9 |
2. 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
19.按右图所示的程序框图运算,若输入 x=200,则输出 k 的值是( )
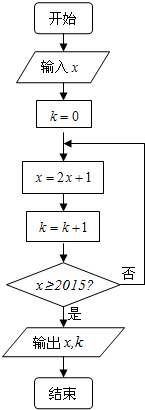

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.在△ABC中,a,b,c分别为内角A,B,C的对边,若2b=a+c,且B=$\frac{π}{4}$,则cosA-cosC的值为( )
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | $\root{4}{2}$ | D. | ±$\root{4}{2}$ |
16.P是双曲线$\frac{x^2}{16}-\frac{y^2}{20}=1$上一点,F1,F2分别是双曲线左右焦点,若|PF1|=9,则|PF2|=( )
| A. | 1 | B. | 17 | C. | 1或17 | D. | 以上答案均不对 |
20.行如图所示的程序框图,若输入a=390,b=156,则输出a=( )
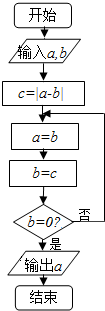

| A. | 26 | B. | 39 | C. | 78 | D. | 156 |
1.已知集合A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
 如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.
如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.