题目内容

1．设F是双曲线$\frac{x^2}{4}$-$\frac{y^2}{12}$=1的左焦点，A（1，4），P是双曲线右支上的动点，则|PF|+|PA|的最小值为（　　）
A．5B．5+4$\sqrt{3}$C．7D．9

分析 根据A点在双曲线的两支之间，根据双曲线的定义求得，|PF|-|PF′|=2a=4，进而根据PA|+|PF′|≥|AF′|=5，两式相加求得答案．

解答 解：∵A点在双曲线的两支之间，且双曲线右焦点为F′（4，0），
∴由双曲线定义可得，|PF|-|PF′|=2a=4，
而|PA|+|PF′|≥|AF′|=5，
两式相加得|PF|+|PA|≥9，
当且仅当A、P、F′三点共线时等号成立．
则|PF|+|PA|的最小值为9．
故选：D．

点评 本题主要考查了双曲线的定义，考查了学生对双曲线定义的灵活运用，同时考查两点间线段最短，属于中档题．

练习册系列答案
相关题目
1．已知等差数列{an}中，a1=3，a19=39，则S26=728．
12．当x＞-1时，函数y=x+$\frac{1}{x+1}$的最小值是1．
9．如图，该程序运行后输出的结果为是（　　） 
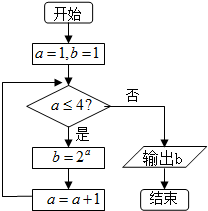
A．2B．4C．8D．16
16．已知xi∈[0，π]，i=1，2，3，…，n，则有
①sinx1=sinx1
②sinx1+sinx2≤2sin$\frac{{{x_1}+{x_2}}}{2}$
③sinx1+sinx2+sinx3≤3sin$\frac{{{x_1}+{x_2}+{x_3}}}{3}$
④sinx1+sinx2+sinx3+sinx4≤4sin$\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}$
由上述结论类比，猜想得到一般的结论是：$sin{x_1}+sin{x_2}+…+sin{x_n}≤nsin\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$．
6．如果执行下面的程序框图，输出的S=240，则判断框中为（　　）
A．k≥15？B．k≤16？C．k≤15？D．k≥16？
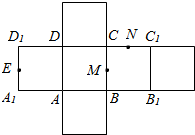13．如图为正方体ABCD-A1B1C1D1的平面展开图，其中E、M、N分别为A1D1、BC、CC1的中点，
（Ⅰ） 作出该正方体的水平放置直观图；
（Ⅱ） 求证：平面BEC1∥平面D1MN．
10．双曲线C：x2-$\frac{{y}^{2}}{6}$=1的左焦点为F，双曲线与直线l：y=kx交于A、B两点，且∠AFB=$\frac{π}{3}$，则$\overrightarrow{FA}$•$\overrightarrow{FB}$=（　　）
A．2B．4C．8D．16
11．对于任意的x1，x2∈R，且x1≠x2，若$f（x）={（{\frac{1}{2}}）^x}，m=\frac{{f（{x_1}）+f（{x_2}）}}{2}，n=f（{\frac{{{x_1}+{x_2}}}{2}}）$，则m与n的大小关系为m＞n．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网