题目内容
3. 如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.
如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.(1)用向量法证明平面A1BD∥平面B1CD1;
(2)用向量法证明MN⊥面A1BD.
分析 (1)建立如图所示的坐标系,设正方体的棱长为2,求出平面A1BD、平面B1CD1的法向量,证明法向量平行,即可证明结论;
(2)求出$\overrightarrow{MN}$=(-1,1,1),可得$\overrightarrow{MN}$∥$\overrightarrow{m}$,即可证明结论.
解答 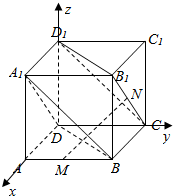 证明:(1)建立如图所示的坐标系,设正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),C(0,2,0),D1(0,0,2),
证明:(1)建立如图所示的坐标系,设正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),C(0,2,0),D1(0,0,2),
设平面A1BD的法向量为$\overrightarrow{m}$=(x,y,z),
∵$\overrightarrow{D{A}_{1}}$=(2,0,2),$\overrightarrow{DB}$=(2,2,0),
∴$\left\{\begin{array}{l}{2x+2z=0}\\{2x+2y=0}\end{array}\right.$,
∴取$\overrightarrow{m}$=(-1,1,1),
同理平面B1CD1的法向量为$\overrightarrow{n}$=(-1,1,1),
∴$\overrightarrow{m}∥\overrightarrow{n}$,
∴平面A1BD∥平面B1CD1;
(2)∵M、N分别为AB、B1C的中点,
∴$\overrightarrow{MN}$=(-1,1,1),
∴$\overrightarrow{MN}$∥$\overrightarrow{m}$,
∴MN⊥面A1BD.
点评 本题考查平面与平面平行的证明,考查直线与平面垂直,正确建立坐标系,求出平面的法向量是关键.

练习册系列答案
相关题目
15.执行如图的程序框图,输出的结果为( )
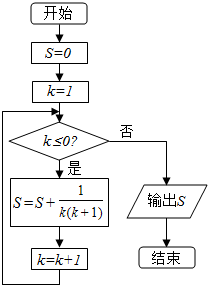

| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{9}{8}$ |
12.已知全集U={x∈N*|x<9 },集合∁U(A∪B)={1,3},A∩∁UB={2,4},则集合B等于( )
| A. | {1,3,5,6,7,8} | B. | {2,4,5,6,7,8} | C. | {5,6,7,8} | D. | {1,2,3,4} |
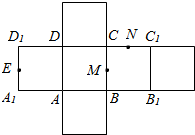 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,