题目内容
2. 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
分析 画图,塔底B测得高楼楼顶C的仰角为60°,所以∠DBC=60°=∠BCE,在高楼楼顶C测得塔顶A俯角为30°,所以∠ECA=30°,故∠ACB=∠ABC=30°∴AC=AB=40,作AF⊥CD,解直角三角形AFC求得FC,再加上FD即得CD的长.
解答  解:∵∠DBC=∠BCE=60°,∠ACE=30°,
解:∵∠DBC=∠BCE=60°,∠ACE=30°,
∴∠ACB=∠BCE-∠ACE=30°,∠ABC=90°-∠DBC=30°,
∴AC=AB=20
作AF⊥CD于点F,∵∠CAF=∠ACE=30°∴CF=$\frac{1}{2}$AC=10,
∴CD=CF+FD=CF+AB=20+10=30
故选:A.
点评 本题考查三角形的应用,主要通过构造出可解的三角形,利用正弦,余弦定理及勾股定理求得相应边长或角度.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
7.给出一个程序框图,则输出x的值是( )


| A. | 39 | B. | 41 | C. | 43 | D. | 45 |
12.已知全集U={x∈N*|x<9 },集合∁U(A∪B)={1,3},A∩∁UB={2,4},则集合B等于( )
| A. | {1,3,5,6,7,8} | B. | {2,4,5,6,7,8} | C. | {5,6,7,8} | D. | {1,2,3,4} |
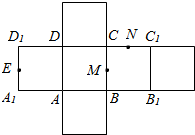 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,