题目内容
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(1)求
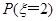 ;
;(2)求随机变量
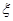 的分布列和数学期望.
的分布列和数学期望.
(1) 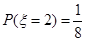 ;(2)
;(2)ξ 2 3 4 P 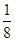
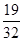
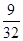
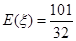 .
.
解析试题分析:(1)先求出基本事件总的个数 ,再求出满足条件的子事件(只能取表格第1,2列中的数字作为密码)的个数为
,再求出满足条件的子事件(只能取表格第1,2列中的数字作为密码)的个数为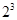 ,由古典概型概率公式求解;(2) 先写出ξ的取值,再结合
,由古典概型概率公式求解;(2) 先写出ξ的取值,再结合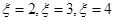 的实际意义,分别求出相应的概率值,注意写出分布列需验证概率和是否为1,再由公式求期望值.
的实际意义,分别求出相应的概率值,注意写出分布列需验证概率和是否为1,再由公式求期望值.
试题解析:(1)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
∴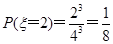 . 5分
. 5分
(2)由题意可知ξ的取值为2,3,4三种情形.
若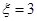 ,注意表格的第一排总含有数字1,第二排总含有数字2,则密码中只可能取数字1,2,3或1,2,4.
,注意表格的第一排总含有数字1,第二排总含有数字2,则密码中只可能取数字1,2,3或1,2,4.
∴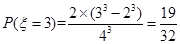 . 8分
. 8分
若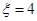 ,
, 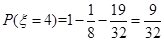 , 10分
, 10分
∴ξ的分布列为:
∴ξ 2 3 4 P 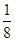
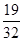
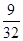
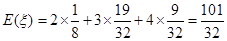 . 12分
. 12分
考点:1.古典概型;2.离散型随机变量的分布列与期望.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
(2)记
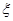 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求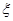 的分布列及期望
的分布列及期望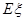 .
.  的一元二次方程
的一元二次方程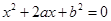 .
. 是从
是从 、
、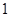 、
、 、
、 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从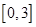 任取的一个数,
任取的一个数,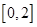 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.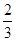 .
.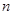 个红球(
个红球(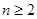 且
且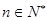 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖. 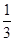 ,求
,求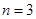 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为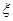 ,试写出
,试写出