题目内容
1．已知不交于同一点的三条直线l1：4x+y-4=0，l2：mx+y=0，l3：x-my-4=0（1）当这三条直线不能围成三角形时，求实数m的值．
（2）当l3与l1，l2都垂直时，求两垂足间的距离．
分析 （1）三条直线不能围成三角形时，至少有两直线平行，分类讨论可得；
（2）当l3与l1，l2都垂直时可得m值，两垂足间的距离即为平行线l1和l2的距离，由平行线间的距离公式可得．
解答 解：（1）三条直线不能围成三角形时，至少有两直线平行，
当直线l1和l2平行时，4-m=0，解得m=4；
当直线l2和l3平行时，-m2-1=0，无解；
当直线l1和l3平行时，-4m-1=0，解得m=-$\frac{1}{4}$；
综上可得m=4或m=-$\frac{1}{4}$；
（2）当l3与l1，l2都垂直时，m=-4，
两垂足间的距离即为平行线l1和l2的距离，
∴d=$\frac{4}{\sqrt{{4}^{2}+1}}$=$\frac{4\sqrt{17}}{17}$
点评 本题考查直线的一般式方程和平行垂直关系，属基础题．
练习册系列答案
相关题目
12．焦点为（0，±3），且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线的双曲线方程是（ ）
| A． | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B． | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C． | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D． | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
16．下列说法不正确的是（ ）
| A． | 圆柱的侧面展开图是一个矩形 | |
| B． | 圆锥中过圆锥轴的截面是一个等腰三角形 | |
| C． | 直角三角形绕它的一边旋转一周而形成的曲面所围成的几何体是一个圆锥 | |
| D． | 用一个平面截一个圆柱，所得截面可能是矩形 |
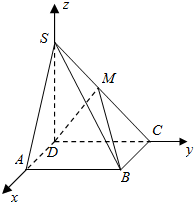如图，在四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=$\sqrt{2}$，DC=SD=2，点M在侧棱SC上，∠ABM=60°．若以DA，DC，DS，分别为x轴，y轴，z轴建立如图所示的空间直角坐标系D-xyz，则M的坐标为（0，1，1）．