题目内容
9.已知函数f(x)=$\frac{x^2}{{\sqrt{x+1}}}$,g(x)=$\frac{{\sqrt{x+1}}}{x}$,则f(x)•g(x)=x,x∈(-1,0)∪(0,+∞).分析 直接将f(x),g(x)代入约分即可.
解答 解:∵函数f(x)=$\frac{x^2}{{\sqrt{x+1}}}$,g(x)=$\frac{{\sqrt{x+1}}}{x}$,
∴f(x)•g(x)=x,x∈(-1,0)∪(0,+∞),
故答案为:x,x∈(-1,0)∪(0,+∞).
点评 本题考查了求函数的解析式问题,考查函数的定义域问题,是一道基础题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
20.将函数f(x)=sin2x的图象向左平移$\frac{π}{4}$个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是( )
| A. | (kπ-$\frac{π}{2}$,kπ)(k∈Z) | B. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
17.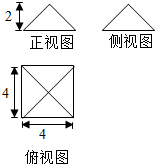 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )
 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
4.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(3)=0,当x<0时,xf′(x)+f(x)>0,则有( )
| A. | f(-3)<f(1)<f(2) | B. | f(2)<f(-3)<f(1) | C. | f(1)<f(-3)<f(2) | D. | f(-3)<f(2)<f(1) |
19.已知等差数列的首项为a1,公差为d.则该数列的通项公式为( )
| A. | an=a1+d(n+1) | B. | an=a1+dn | C. | an=a1+d(n-1) | D. | an=a1+d(n-2) |
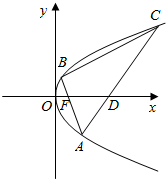 已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.
已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.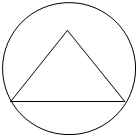 棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.
棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.