题目内容
11.已知函数f(x)=2cosx(cosx+$\sqrt{3}$sinx).(1)求函数f(x)的单调递减区间和对称中心;
(2)若0<α<π,且f($\frac{α}{2}$)=$\frac{1}{3}$,求cosα的值.
分析 (1)展开表达式,利用二倍角与两角和的正弦函数,化为一个角的一个三角函数的形式,结合正弦函数的单调增区间求出函数的单调减区间即可.
(2)化简已知可得sin(α+$\frac{π}{6}$)=-$\frac{1}{3}$,结合角的范围利用同角三角函数关系式可求cos(α+$\frac{π}{6}$)的值,由cosα=cos[(α+$\frac{π}{6}$)-$\frac{π}{6}$]利用两角差的余弦函数公式即可求值得解.
解答 解:(1)∵函数f(x)=2cosx($\sqrt{3}$sinx+cosx)=$\sqrt{3}$sin2x+2cos2x=2sin(2x+$\frac{π}{6}$)+1.
∵2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,
∴x∈[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z,
∴函数的单调减区间为:[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z,
(2)∵0<α<π,且f($\frac{α}{2}$)=2sin(α+$\frac{π}{6}$)+1=$\frac{1}{3}$,解得:sin(α+$\frac{π}{6}$)=-$\frac{1}{3}$,
又∵$\frac{π}{6}$<α+$\frac{π}{6}$<$\frac{7π}{6}$,
∴可得:π<α+$\frac{π}{6}$<$\frac{7π}{6}$,cos(α+$\frac{π}{6}$)=-$\sqrt{1-si{n}^{2}(α+\frac{π}{6})}$=-$\frac{2\sqrt{2}}{3}$,
∴cosα=cos[(α+$\frac{π}{6}$)-$\frac{π}{6}$]=cos(α+$\frac{π}{6}$)cos$\frac{π}{6}$+sin(α+$\frac{π}{6}$)sin$\frac{π}{6}$=(-$\frac{2\sqrt{2}}{3}$)×$\frac{\sqrt{3}}{2}$+(-$\frac{1}{3}$)×$\frac{1}{2}$=-$\frac{2\sqrt{6}+1}{6}$.
点评 本题主要考查了三角函数恒等变换的应用,同角三角函数关系式的应用,函数的单调增区间的求法,考查计算能力,熟练记忆和灵活应用相关公式是解题的关键,属于中档题.

| A. | an=a1+d(n+1) | B. | an=a1+dn | C. | an=a1+d(n-1) | D. | an=a1+d(n-2) |
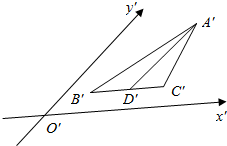 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AD,最短的是AC |