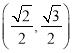Question

【题目】(导学号：05856306)

在△ABC中，内角A，B，C的对边分别为a，b，c，已知，且b＝5，acos C＝－1.

(Ⅰ)求角A；

(Ⅱ)求△ABC的面积．

Answer 1

【答案】(1) (2)15

【解析】试题分析：（1）先化简，再根据正弦定理和余弦定理即可求出A的值；

（2）由余弦定理和b=5，acosC=﹣1，求出c，再根据三角面积公式即可求出．

试题解析：

(Ⅰ)由正弦定理得＝，＝，

所以＝1－，整理得b2＋c2－a2＝bc，

所以cos A＝＝，又A∈(0，π)，所以A＝.

(Ⅱ)因为acos C＝－1，所以由余弦定理得a·＝－1，

整理得a2－c2＝－b2－2b＝－35，把b＝5，a2－c2＝－35，代入b2＋c2－a2＝bc，得

25＝－35＋5c，解得c＝12,

所以S△ABC＝bcsin A＝×5×12×＝15.