Question

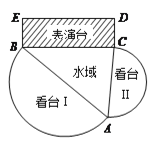
【题目】在一水域上建一个演艺广场.演艺广场由看台Ⅰ，看台Ⅱ，三角形水域，及矩形表演台四个部分构成（如图）.看台Ⅰ，看台Ⅱ是分别以， 为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍；矩形表演台中， 米；三角形水域的面积为平方米.设.

（Ⅰ）当时，求的长；

（Ⅱ）若表演台每平方米的造价为万元，求表演台的最低造价.

Answer 1

【答案】(Ⅰ)40；(Ⅱ)120万元.

【解析】试题分析：（1）根据看台的面积比得出AB，AC的关系，代入三角形的面积公式求出AB，AC，再利用余弦定理计算BC；（2）根据（1）得出造价关于θ的函数，利用导数判断函数的单调性求出最小造价

解析：

（Ⅰ）因为看台Ⅰ的面积是看台Ⅱ的面积的3倍，所以.

在△中， ，所以 .

由余弦定理可得

，即

所以 ， . 当时，

(Ⅱ）设表演台的总造价为万元.因为m，表演台每平方米的造价为0.3万元，所以 ， .

记， .则.

由，解得.

当时， ；当时， .

故在上单调递减，在上单调递增，

从而当 时， 取得最小值，最小值为. 所以 (万元).