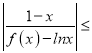题目内容
【题目】(导学号：05856311)[选修4－4：坐标系与参数方程]
已知曲线C1： 
(α为参数)与曲线C2：ρ＝4sin θ(θ为参数)．
(Ⅰ)写出曲线C1的普通方程和曲线C2的直角坐标方程；
(Ⅱ)求C1和C2公共弦的长度．
【答案】(1) C1的普通方程为(x－1)2＋y2＝4，C2的直角坐标方程为x2＋y2－4y＝0 (2) 
【解析】试题分析：（1）利用sin2θ+cos2θ=1消参数得到C1的普通方程，对ρ=4sinθ两边同乘以ρ即可得到曲线C2的普通方程；
（2）曲线C1和C2公共弦所在额直线为2x﹣4y+3=0，求出圆心距，即可求出公共弦长．
试题解析：
(Ⅰ)因为曲线C1：
(α为参数)与曲线C2：ρ＝4sin θ(θ为参数)，
所以C1的普通方程为(x－1)2＋y2＝4，C2的直角坐标方程为x2＋y2－4y＝0.
(Ⅱ)因为C1和C2公共弦所在直线为2x－4y＋3＝0，所以点(1,0)到2x－4y＋3＝0的距离为
，所以公共弦长为2
＝
.
练习册系列答案
相关题目
