题目内容

设AB是椭圆的长轴，点C在椭圆上，且∠CBA=
π
4
．若AB=4，BC=
2
，则椭圆的焦距为（　　）
A．
3
3
B．
2
6
3
C．
4
6
3
D．
2
3
3
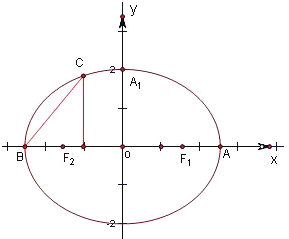
如图，设椭圆的标准方程为
x2
a2
+
y2
b2
=1，
由题意知，2a=4，a=2．
∵∠CBA=
π
4
，BC=
2
，可设C（y0-2，y0），
∵B（-2，0），
∴
BC
=（y0，y0），
∴|
BC
|=
2
y0=
2
，解得y0=1，
∴点C的坐标为C（-1，1），
∵点C在椭圆上，∴
(-1)2
4
+
12
b2
=1，
∴b2=
4
3
，
∴c2=a2-b2=4-
4
3
=
8
3
，c=
2
6
3
，
∴椭圆的焦距为
4
6
3
．
故选：C．
练习册系列答案
相关题目
在等边△ABC中，若以A，B为焦点的椭圆经过点C，则该椭圆的离心率为______．
在平面直角坐标系中，已知△ABC的顶点A（-5，0），B（5，0）且顶点C在椭圆
x2
169
+
y2
144
=1上，则
sinA+sinB
sinC
=______．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F，右顶点为A，点B在椭圆上，且BF⊥x轴，直线AB交y轴于点P．若
AP
=2
PB
，
|AP|=2|PB|，则椭圆的离心率为______．
点A、B分别是椭圆
x2
36
+
y2
20
=1长轴的左、右焦点，点F是椭圆的右焦点．点P在椭圆上，且位于x轴上方，PA⊥PF．
（1）求P点的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．
若椭圆
x2
a2
+
y2
b2
=1（a＞0，b＞0）的两焦点关于直线y=x的对称点均在椭圆内部，则椭圆的离心率e的取值范围为______．
如图，面ABC⊥α，D为AB的中点，|AB|=2，∠CDB=60°，P为α内的动点，且P到直线CD的距离为
3
，则∠APB的最大值为（　　）
A．30°B．60°C．90°D．120°
定点N（1，0），动点A、B分别在图中抛物线y2=4x及椭圆
x2
4
+
y2
3
=1的实线部分上运动，且AB∥x轴，则△NAB的周长l取值范围是（　　）
A．（
2
3
，2）		B．（
10
3
，4）		C．（
51
16
，4）		D．（2，4）
直线l与椭圆
x2
4
+
y2
3
=1相交于两点A，B，弦AB的中点为（-1，1），则直线l的方程为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网