题目内容

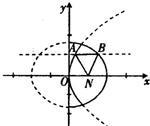
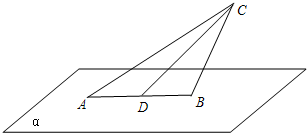
如图，面ABC⊥α，D为AB的中点，|AB|=2，∠CDB=60°，P为α内的动点，且P到直线CD的距离为
3
，则∠APB的最大值为（　　）
A．30°B．60°C．90°D．120°

空间中到直线CD的距离为
3
的点构成一个圆柱面，它和面α相交得一椭圆，所以P在α内的轨迹为一个椭圆，D为椭圆的中心，b=
3
，a=
3
sin60°
=2，则c=1，于是A，B为椭圆的焦点，椭圆上点关于两焦点的张角
在短轴的端点取得最大，故为60°．
故选B．
练习册系列答案
相关题目
已知△ABC的两个顶点A，B的坐标分别是（0，-1），（0，1），且AC，BC所在直线的斜率之积等于m（m≠0）．
（1）求顶点C的轨迹E的方程，并判断轨迹E为何种圆锥曲线；
（2）当m=-
1
2
时，过点F（1，0）的直线l交曲线E于M，N两点，设点N关于x轴的对称点为Q（M，Q不重合）试问：直线MQ与x轴的交点是否为定点？若是，求出定点，若不是，请说明理由．
已知有公共焦点的椭圆与双曲线的中心为原点，焦点在x轴上，左、右焦点分别为F1，F2且它们在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形，双曲线的离心率的取值范围为（1，2），则该椭圆的离心率的取值范围是（　　）
A．（0，
1
3
）		B．（
1
3
，
1
2
）		C．（
1
3
，
2
5
）		D．（
2
5
，1）
设AB是椭圆的长轴，点C在椭圆上，且∠CBA=
π
4
．若AB=4，BC=
2
，则椭圆的焦距为（　　）
A．
3
3
B．
2
6
3
C．
4
6
3
D．
2
3
3
过椭圆
x2
2
+
y2
3
=1的下焦点，且与圆x2+y2-3x+y+
3
2
=0相切的直线的斜率是______．
已知△ABC的顶点B，C在椭圆
x2
3
+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（　　）
A．2
3
B．6C．4
3
D．12
设椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点为F，C为椭圆短轴上的端点，向量
FC
绕F点顺时针旋转90°后得到向量
FC′
，其中C′点恰好落在椭圆右准线上，则该椭圆的离心率为______．
椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的两个焦点为F1（-c，0）、F2（c，0），M是椭圆上一点，且满足
F1M
•
F2M
=0．
（1）求离心率e的取值范围；
（2）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为5
2
，求此时椭圆的方程．
已知定点N（1，0），动点A、B分别在图中抛物线y2=4x及椭圆
x2
4
+
y2
3
=1的实线部分上运动，且AB∥x轴，则△NAB的周长L的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网