题目内容
【题目】已知函数f(x)=mx2-mx-1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
【答案】(1)(-4,0].(2)![]()
【解析】试题分析:(1)先根据二次项系数是否为零分类讨论,再结合二次函数图像确定不等式恒成立的条件,最后求解实数m的取值范围;(2)分类变量将不等式转化为对应函数最值问题: ![]() 的最小值,再根据二次函数求最值,即得实数m的取值范围.
的最小值,再根据二次函数求最值,即得实数m的取值范围.
试题解析:解:(1)由题意可得m=0或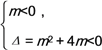 m=0或-4<m<0-4<m≤0.
m=0或-4<m<0-4<m≤0.
故m的取值范围是(-4,0].
(2)要使f(x)<-m+5在[1,3]上恒成立,即m![]() 2+
2+![]() m-6<0在x∈[1,3]上恒成立.
m-6<0在x∈[1,3]上恒成立.
令g(x)=m![]() 2+
2+![]() m-6,x∈[1,3].
m-6,x∈[1,3].
当m>0时,g(x)在[1,3]上是增函数,
所以g(x)max=g(3)7m-6<0,
所以m<![]() ,则0<m<
,则0<m<![]() ;
;
当m=0时,-6<0恒成立;
当m<0时,g(x)在[1,3]上是减函数,
所以g(x)max=g(1)m-6<0,
所以m<6,所以m<0.
综上所述:m的取值范围是![]() .
.

【题目】某学校高三年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(Ⅰ)完成下面的![]() 列联表;
列联表;
不喜欢运动 | 喜欢运动 | 合计 | |
女生 | 50 | ||
男生 | |||
合计 | 100 | 200 |
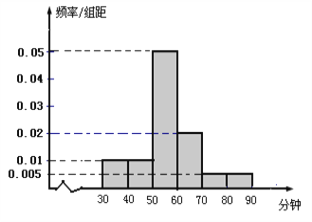
(Ⅱ)在抽取的样本中,调查喜欢运动女生的运动时间,发现她们的运动时间介于30分钟到90分钟之间,右图是测量结果的频率分布直方图,若从区间段![]() 和
和![]() 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() (万元)和销售额
(万元)和销售额![]() (万元)的数据统计如下表:
(万元)的数据统计如下表:
城市 |
|
|
|
|
|
|
|
广告费支出 |
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
(Ⅰ)若用线性回归模型拟合![]() 与
与![]() 关系,求
关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若用对数函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,经计算对数函数回归模型的相关系数约为
,经计算对数函数回归模型的相关系数约为![]() ,请说明选择哪个回归模型更合适,并用此模型预测
,请说明选择哪个回归模型更合适,并用此模型预测![]() 城市的广告费用支出
城市的广告费用支出![]() 万元时的销售额.
万元时的销售额.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 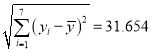 ,
, ![]() ,
, ![]() .
.
参考公式: 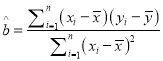 ,
, ![]() .
.
相关系数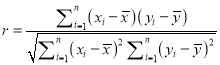 .
.