题目内容
【题目】(2018届高三·湖南十校联考)已知函数f(x)=x+sin x(x∈R),且f(y2-2y+3)+f(x2-4x+1)≤0,则当y≥1时, ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. [1,3![]() -3] D.
-3] D. ![]()
【答案】A
【解析】因为函数f(x)=x+sin x(x∈R)为奇函数,
又f′(x)=1+cos x≥0,
所以函数f(x)在R上单调递增,
则f(x2-4x+1)≤f(-y2+2y-3),
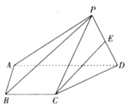
即(x-2)2+(y-1)2≤1,
当y≥1时表示的区域为半圆及其内部.
令k=![]() 其几何意义为过点(-1,0)与半圆相交或相切的直线kx-y+k=0的斜率,
其几何意义为过点(-1,0)与半圆相交或相切的直线kx-y+k=0的斜率,
斜率最小时直线过点(3,1),此时kmin=![]() ,斜率最大时直线刚好与半圆相切,
,斜率最大时直线刚好与半圆相切,
圆心到直线的距离d=![]() =1(k>0),
=1(k>0),
解得kmax=![]() ,故选A.
,故选A.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.