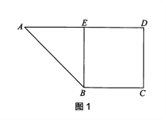
题目内容
【题目】已知关于![]() 的不等式
的不等式![]() (其中
(其中![]() ).
).
(1)当![]() 时,求不等式的解集;
时,求不等式的解集;
(2)若不等式在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)不等式的解集为{x|-4≤x≤![]() }.(2)a的取值范围是
}.(2)a的取值范围是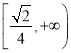
【解析】试题分析: (1)当a=4时,不等式即|2x+1|-|x-1|≤2,分类讨论,去掉绝对值,分别求出解集,再取并集,即得所求;
(2)化简f(x)=|2x+1|-|x-1|的解析式,求出f(x)的最小值,得到关于a的不等式,解得实数a的取值范围.
试题解析:
(1)当a=4时,不等式即为|2x+1|-|x-1|≤2,
当x<-![]() 时,-x-2≤2,得-4≤x<-
时,-x-2≤2,得-4≤x<-![]() ,当-
,当-![]() ≤x≤1时,3x≤2,得-
≤x≤1时,3x≤2,得-![]() ≤x≤
≤x≤![]() ,
,
当x>1时,x≤0,此时x不存在.∴不等式的解集为{x|-4≤x≤![]() }.
}.
(2)∵设f(x)=|2x+1|-|x-1|=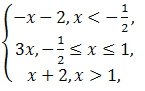
∴f(x)∈[-![]() ,+∞),即f(x)的最小值为-
,+∞),即f(x)的最小值为-![]() .若f(x)≤log2a有解,则log2a≥-
.若f(x)≤log2a有解,则log2a≥-![]() ,
,
解得![]() 即a的取值范围是
即a的取值范围是![]()

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.