题目内容
【题目】已知函数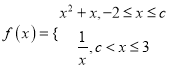 ,若
,若![]() ,则
,则![]() 的值域是______;若
的值域是______;若![]() 的值域是
的值域是![]() ,则实数
,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】 ![]()
![]()
【解析】c=0时,f(x)=x2+x=(x+![]() , f(x)在[-2,-
, f(x)在[-2,-![]() ] 递减,在(-
] 递减,在(-![]() ,0)递增,
,0)递增,
可得f(-2)取得最大值,且为2,最小值为![]() , 当0<x≤3时,f(x)=
, 当0<x≤3时,f(x)=![]() 递减,可得f(3)=
递减,可得f(3)=![]() , 则f(x)∈[
, 则f(x)∈[![]() ,+
,+![]() ,综上可得f(x)的值域为
,综上可得f(x)的值域为![]() . ∵函数y=x2+x在区间
. ∵函数y=x2+x在区间
[-2,--![]() ] 上是减函数,在区间(-
] 上是减函数,在区间(-![]() , ,1]上是增函数,∴当x∈[-2,0)时,函数f(x)最小值为f(-
, ,1]上是增函数,∴当x∈[-2,0)时,函数f(x)最小值为f(-![]() )=-
)=-![]() , 最大值是f(-2)=2;由题意可得c>0,∵当c<x≤3时,f(x)=
, 最大值是f(-2)=2;由题意可得c>0,∵当c<x≤3时,f(x)=![]() 是减函数且值域为[
是减函数且值域为[![]() , 当f(x)的值域是
, 当f(x)的值域是![]() , 可得
, 可得![]() ,
,
故答案为(1). ![]() . (2).
. (2). ![]() .
.

练习册系列答案
相关题目