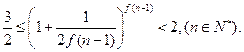题目内容
对任意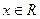 ,给定区间
,给定区间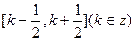 ,设函数
,设函数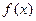 表示实数
表示实数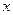 与
与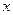 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
(1)当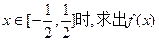 的解析式;当
的解析式;当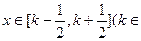 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的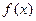 的解析式,并说明理由; (2)判断函数
的解析式,并说明理由; (2)判断函数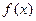
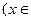 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;
(3)求方程 的实根.(要求说明理由)
的实根.(要求说明理由)
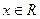 ,给定区间
,给定区间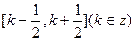 ,设函数
,设函数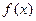 表示实数
表示实数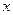 与
与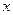 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
|
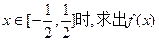 的解析式;当
的解析式;当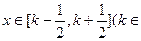 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的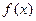 的解析式,并说明理由; (2)判断函数
的解析式,并说明理由; (2)判断函数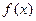
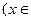 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;(3)求方程
 的实根.(要求说明理由)
的实根.(要求说明理由)(1)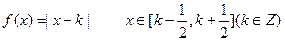
(2)证明见解析。
(3)若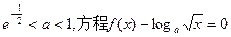 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.
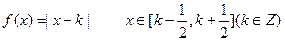
(2)证明见解析。
(3)若
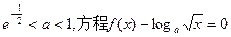 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.(Ⅰ)当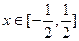 时,由定义知:
时,由定义知: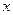 与0距离最近,
与0距离最近,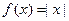
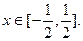
当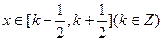 时,由定义知:
时,由定义知: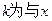 最近的一个整数,故
最近的一个整数,故
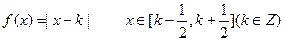
(Ⅱ)对任何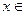 R,函数
R,函数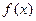 都存在,且存在
都存在,且存在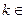 Z,
Z,
满足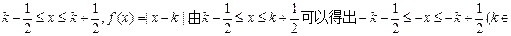 Z)
Z)
即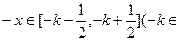 Z).
Z).
由(Ⅰ)的结论,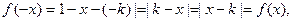
即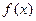 是偶函数.
是偶函数.
(Ⅲ)(理科)解: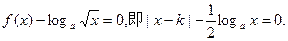
(1)当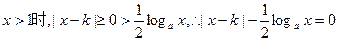 没有大于1的实根;
没有大于1的实根;
(2)容易验证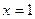 为方程
为方程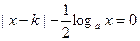 的实根;
的实根;
(3)当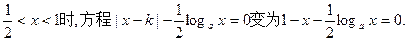
设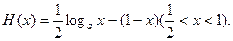
则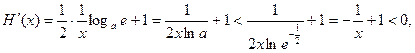
所以当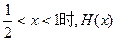 为减函数,
为减函数,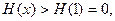
所以方程没有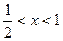 的实根;
的实根;
(4)当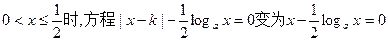
设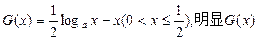 为减函数,
为减函数,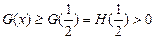 ,
,
所以方程没有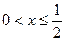 的实根.
的实根.
综上可知,若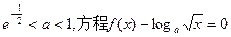 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.
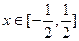 时,由定义知:
时,由定义知: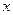 与0距离最近,
与0距离最近,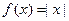
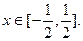
当
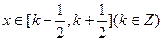 时,由定义知:
时,由定义知: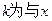 最近的一个整数,故
最近的一个整数,故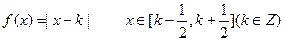
(Ⅱ)对任何
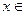 R,函数
R,函数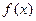 都存在,且存在
都存在,且存在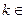 Z,
Z,满足
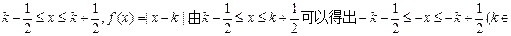 Z)
Z)即
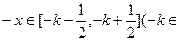 Z).
Z).由(Ⅰ)的结论,
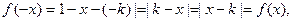
即
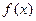 是偶函数.
是偶函数.(Ⅲ)(理科)解:
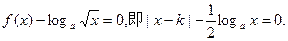
(1)当
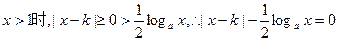 没有大于1的实根;
没有大于1的实根;(2)容易验证
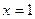 为方程
为方程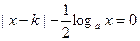 的实根;
的实根;(3)当
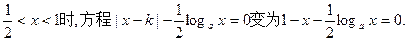
设
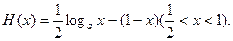
则
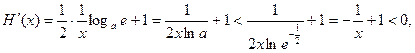
所以当
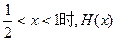 为减函数,
为减函数,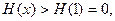
所以方程没有
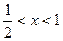 的实根;
的实根;(4)当
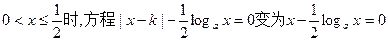
设
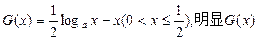 为减函数,
为减函数,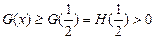 ,
,所以方程没有
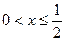 的实根.
的实根. 综上可知,若
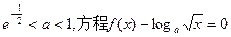 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.
练习册系列答案
相关题目
 是函数
是函数 的一个极值,称点
的一个极值,称点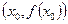 是函数
是函数
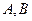 ,求
,求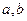 所满足的关系;
所满足的关系;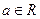 ,求
,求 表示的区域内时实数
表示的区域内时实数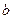 的范围.
的范围.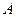 ,且存在
,且存在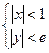 表示的区域内,证明:
表示的区域内,证明: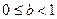 .
.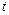 元(其中
元(其中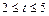 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为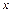 元(
元(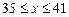 ),根据市场调查,日销售量与
),根据市场调查,日销售量与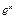 (
(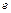 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.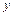 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价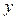 最大,并求
最大,并求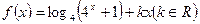 是偶函数.
是偶函数.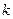 的值;
的值;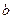 ,函数
,函数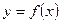 的图象与直线
的图象与直线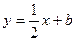 最多只有一个交点.
最多只有一个交点. 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)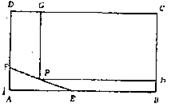
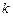 和
和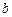 ,使得函数
,使得函数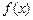 和
和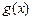 对其定义域上的任意实数
对其定义域上的任意实数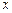 分别满足:
分别满足: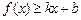 和
和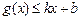 ,则称直线
,则称直线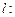
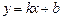 为
为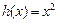 ,
,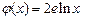 (其中
(其中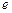 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断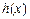 与
与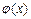 间的隔离直线方程为 .
间的隔离直线方程为 .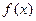
 .
.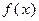 的解析式;
的解析式;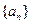 满足:
满足: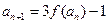 (
(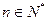 ),且
),且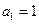 , 求数列
, 求数列