题目内容
.已知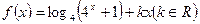 是偶函数.
是偶函数.
(1)求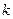 的值;
的值;
(2)证明:对任意实数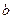 ,函数
,函数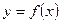 的图象与直线
的图象与直线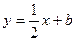 最多只有一个交点.
最多只有一个交点.
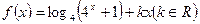 是偶函数.
是偶函数.(1)求
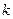 的值;
的值;(2)证明:对任意实数
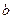 ,函数
,函数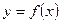 的图象与直线
的图象与直线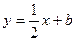 最多只有一个交点.
最多只有一个交点. (1) ;(2)同解析。
;(2)同解析。
 ;(2)同解析。
;(2)同解析。(1)解:由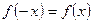 ,得
,得 .
.
(2)证明:由(1)得 ,令
,令 ,得
,得 ,
,
假设方程有两个不等的实数根,则 ①,
①, ②.
②.
两式相减得 ,
,
因为 ,所以
,所以 ,代入①或②不成立,假设错误,命题成立.
,代入①或②不成立,假设错误,命题成立.
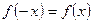 ,得
,得 .
.(2)证明:由(1)得
 ,令
,令 ,得
,得 ,
,假设方程有两个不等的实数根,则
 ①,
①, ②.
②.两式相减得
 ,
,因为
 ,所以
,所以 ,代入①或②不成立,假设错误,命题成立.
,代入①或②不成立,假设错误,命题成立.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
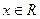 ,给定区间
,给定区间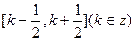 ,设函数
,设函数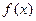 表示实数
表示实数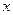 与
与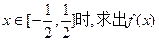 的解析式;当
的解析式;当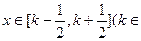 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的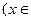 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论; 的实根.(要求说明理由)
的实根.(要求说明理由)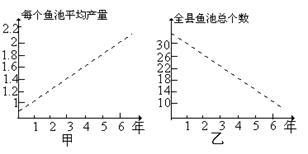
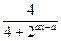 在[0,1]上的最小值为
在[0,1]上的最小值为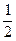 ,
,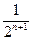 (n∈N
(n∈N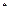 )
)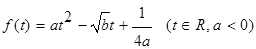 的最大值为正实数,集合
的最大值为正实数,集合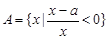 ,集合
,集合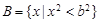 。
。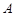 和
和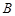 ;
;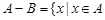 且
且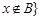 。
。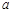 ,
,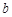 ,
,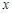 均为整数,且
均为整数,且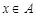 。
。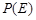 为
为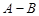 的概率,
的概率,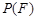 为
为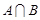 的概率,写出
的概率,写出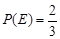 ,
,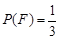 。
。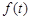 中,
中,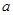 ,
,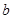 是(2)中
是(2)中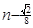 ,n]上的最 大值函数
,n]上的最 大值函数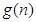 的表达式。
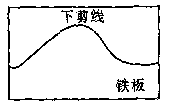
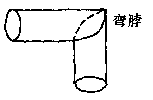
的表达式。 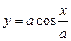 的一个周期的图象,问弯脖的直径为12
的一个周期的图象,问弯脖的直径为12 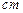 时,
时, 应是多少
应是多少
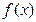 不是常数函数,对于
不是常数函数,对于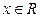 有
有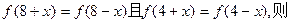
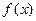 的周期是 .
的周期是 .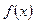 的定义域为
的定义域为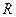 ,对任意实数
,对任意实数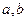 满足
满足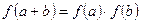 .
. ,试求
,试求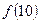 ;(2)设当
;(2)设当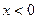 时,
时,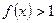 ,试解不等式
,试解不等式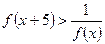 .
. .
.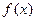 的解析式;
的解析式;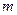 满足:
满足: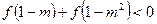 , 求
, 求