题目内容
如果 是函数
是函数 的一个极值,称点
的一个极值,称点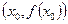 是函数
是函数 的一个极值点.已知函数
的一个极值点.已知函数
(1)若函数 总存在有两个极值点
总存在有两个极值点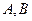 ,求
,求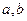 所满足的关系;
所满足的关系;
(2)若函数 有两个极值点
有两个极值点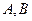 ,且存在
,且存在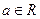 ,求
,求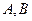 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数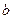 的范围.
的范围.
(3)若函数 恰有一个极值点
恰有一个极值点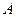 ,且存在
,且存在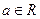 ,使
,使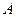 在不等式
在不等式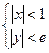 表示的区域内,证明:
表示的区域内,证明: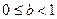 .
.
 是函数
是函数 的一个极值,称点
的一个极值,称点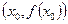 是函数
是函数 的一个极值点.已知函数
的一个极值点.已知函数
(1)若函数
 总存在有两个极值点
总存在有两个极值点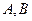 ,求
,求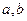 所满足的关系;
所满足的关系;(2)若函数
 有两个极值点
有两个极值点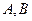 ,且存在
,且存在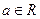 ,求
,求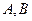 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数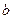 的范围.
的范围.(3)若函数
 恰有一个极值点
恰有一个极值点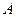 ,且存在
,且存在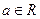 ,使
,使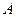 在不等式
在不等式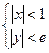 表示的区域内,证明:
表示的区域内,证明: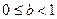 .
.(1)同解析(2)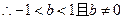 (3) 满足题意
(3) 满足题意 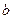 的范围为
的范围为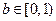 .
.
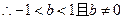 (3) 满足题意
(3) 满足题意 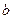 的范围为
的范围为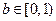 .
.(1)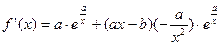
令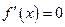 得
得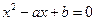
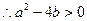 又
又 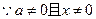
 ………………3分
………………3分
(2)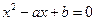 在
在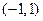 有两个不相等的实根.
有两个不相等的实根.
即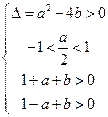 得
得 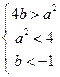
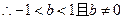 ………………7分
………………7分
(3)由①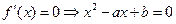
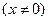
①当 在
在 左右两边异号
左右两边异号
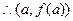 是
是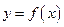 的唯一的一个极值点
的唯一的一个极值点
由题意知 即
即 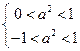 即
即 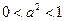
存在这样的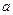 的满足题意
的满足题意 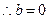 符合题意 ………………9分
符合题意 ………………9分
②当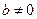 时,
时,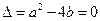 即
即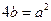
这里函数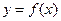 唯一的一个极值点为
唯一的一个极值点为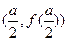
由题意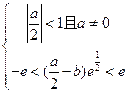
即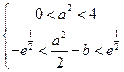 即
即 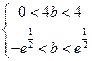
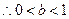 ………………………………13分
………………………………13分
综上知:满足题意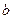 的范围为
的范围为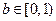 . ……………………………14分
. ……………………………14分
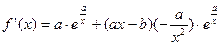
令
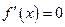 得
得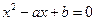
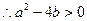 又
又 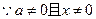
 ………………3分
………………3分(2)
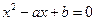 在
在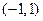 有两个不相等的实根.
有两个不相等的实根.即
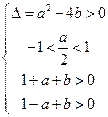 得
得 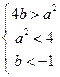
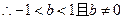 ………………7分
………………7分(3)由①
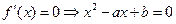
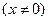
①当
 在
在 左右两边异号
左右两边异号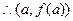 是
是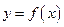 的唯一的一个极值点
的唯一的一个极值点由题意知
 即
即 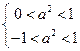 即
即 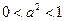
存在这样的
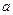 的满足题意
的满足题意 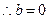 符合题意 ………………9分
符合题意 ………………9分②当
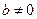 时,
时,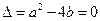 即
即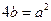
这里函数
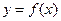 唯一的一个极值点为
唯一的一个极值点为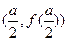
由题意
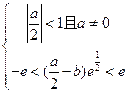
即
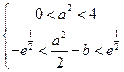 即
即 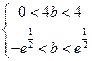
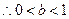 ………………………………13分
………………………………13分综上知:满足题意
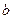 的范围为
的范围为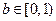 . ……………………………14分
. ……………………………14分
练习册系列答案
相关题目
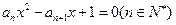 有两个实根
有两个实根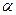 和
和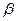 ,
,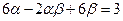 .
.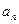 表示
表示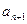 ;
;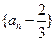 是等比数列;
是等比数列;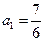 时,求数列
时,求数列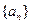 的通项公式.
的通项公式.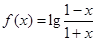 ,且
,且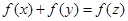 ,则
,则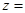 ( ).
( ).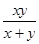
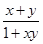
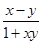
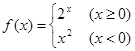 ,若
,若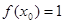 ,则
,则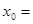 .
.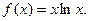
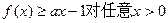 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;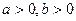 ,证明:
,证明: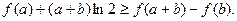
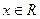 ,给定区间
,给定区间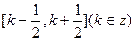 ,设函数
,设函数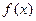 表示实数
表示实数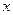 与
与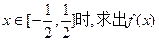 的解析式;当
的解析式;当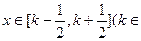 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的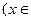 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论; 的实根.(要求说明理由)
的实根.(要求说明理由)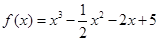 ,若对任意
,若对任意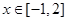 有
有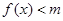 成立,则实数
成立,则实数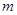 的取值范围是
的取值范围是 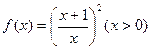 .
.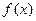 的反函数
的反函数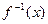 ;
;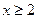 时,不等式
时,不等式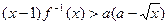 恒成立,试求实数
恒成立,试求实数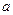 的范围.
的范围.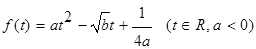 的最大值为正实数,集合
的最大值为正实数,集合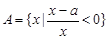 ,集合
,集合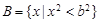 。
。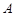 和
和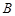 ;
;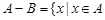 且
且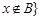 。
。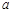 ,
,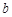 ,
,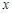 均为整数,且
均为整数,且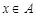 。
。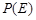 为
为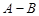 的概率,
的概率,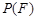 为
为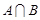 的概率,写出
的概率,写出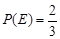 ,
,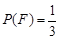 。
。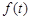 中,
中,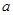 ,
,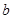 是(2)中
是(2)中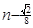 ,n]上的最 大值函数
,n]上的最 大值函数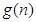 的表达式。
的表达式。