题目内容
5.已知数列{an}的前n项和为Sn,且a1=0,对任意的n∈N*,都有nan+1=Sn+n(n+1),求通项公式.分析 通过nan+1=Sn+n(n+1),可得nan=Sn+n(n-1),两式相减计算即得结论.
解答 解:∵nan+1=Sn+n(n+1),
∴(n+1)an+1=an+1+Sn+n(n+1)=Sn+1+n(n+1),
∴nan=Sn+n(n-1),
两式相减得:(n+1)an+1-nan=Sn+1+n(n+1)-[Sn+n(n-1)],
化简得:an+1-an=2,
又∵a1=0,
∴an=2n-2.
点评 本题考查求数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20.已知条件p:|x+1|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | a≤-3 |
15.$\frac{3+2i}{2-3i}$( )
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
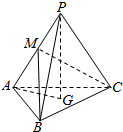 如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.
如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.