题目内容
19．
如图：在三棱锥P-ABC中，AB=AC=2$\sqrt{10}$，BC=4，PC=2$\sqrt{11}$，点P在平面ABC内的射影恰为△ABC的重心G，M为侧棱AP上一动点．（1）求证：平面PAG⊥平面BCM；
（2）当M为AP中点时，求三棱锥M-PGC的体积．
分析 （1）取BC中点D，连接AD、PD，由已知条件推导出PG⊥BC，AG⊥BC，从而得到BC⊥平面PAG，由此能够证明平面PAG⊥平面BCM．
（2）利用三棱锥M-PGC的体积=$\frac{1}{2}{V}_{A-PGC}$=$\frac{1}{2}{V}_{P-AGC}$，可得三棱锥M-PGC的体积．
解答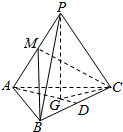 
（1）证明：取BC中点D，连接AD、PD，
∵PG⊥平面ABC，∴PG⊥BC，
等腰△ABC中，G为重心，∴AG⊥BC，
∴BC⊥平面PAG，
∴平面PAG⊥平面BCM；
（2）解：△ABC中，AD=6，∴GD=2，
∵BC⊥平面PAG，∴CD⊥PD，
∴PD=2$\sqrt{10}$，∴GP=6，
∴三棱锥M-PGC的体积=$\frac{1}{2}{V}_{A-PGC}$=$\frac{1}{2}{V}_{P-AGC}$=$\frac{1}{2}×\frac{1}{3}×4×6$=4．
点评 本题考查平面与平面垂直的证明，考查三棱锥M-PGC的体积的求法，正确运用平面PAG⊥平面BCM的判定是关键．
练习册系列答案
相关题目
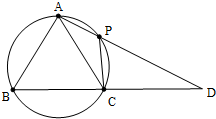在△ABC中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D．
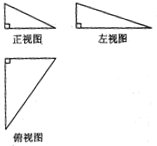一个三棱锥的三视图如图所示，其正视图、左视图、俯视图的面积分别是1，2，4，则这个几何体的外接球的表面积为21π．
如图，已知点S（-2，0）和圆O：x2+y2=4，ST是圆O的直径，从左到右M、O和N依次是ST的四等分点，P（异于S，T）是圆O上的动点，PD⊥ST，交ST于D，$\overrightarrow{PE}$=λ$\overrightarrow{ED}$，直线PS与TE交于C，|CM|+|CN|为定值．
A，B两名学生在5次英语口语测试中的成绩统计如茎叶图所示（十位作为茎）．