题目内容
【题目】已知椭圆
的离心率为
，短轴长为4.
（1）求椭圆
的方程；
（2）过点
作两条直线，分别交椭圆于
两点（异于
），当直线
，
的斜率之和为4时，直线
恒过定点，求出定点的坐标.
【答案】（1）
（2）见解析
【解析】
（1）首先根据题中所给的条件，得到
所满足的等量关系式，求解即可；
（2）分直线AB的斜率存在与不存在两种情况进行讨论，写出直线的方程
，，将其与椭圆方程联立，根据题中的条件，求得
，从而求得直线所过的定点为
，当直线AB斜率不存在时，验证也过该点，得证.
（1）由题意知：
，
，
.
解得
，
，
，所以椭圆方程为.
（2）当直线
的斜率存在时，设直线方程为，
，
.
由
，得
，
联立
，消去
得
，由题意知二次方程有两个不等实根，
∴
，
.
代入
得
，整理得
.
∵
，∴，∴
，
，所以直线恒过定点.
当直线的斜率不存在时，设直线的方程为
，
，
，其中
，∴
.由，得
，∴
.
∴当直线的斜率不存在时，直线也过定点.
综上所述，直线恒过定点.
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在
内，发布成绩使用等级制，各等级划分标准见下表．
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定：A，B，C三级为合格等级，D为不合格等级为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．
按照
，
，
，
，
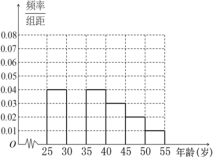
的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示
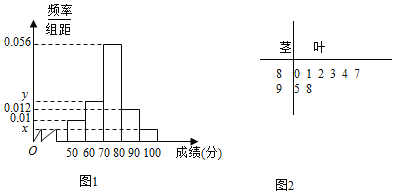
求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；
根据频率分布直方图，求成绩的中位数
精确到
；
在选取的样本中，从A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A等级的概率．
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)
男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:
，
，
，
，
，
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
