题目内容
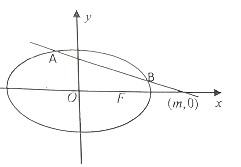
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
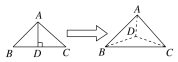
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是( )
A.①②④B.①②③
C.②③④D.①③④
【答案】B
【解析】
根据翻折后垂直关系得BD⊥平面ADC,即得BD⊥AC,再根据计算得△BAC是等边三角形,最后可确定选项.
由题意知,BD⊥平面ADC,故BD⊥AC,①正确;AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD,所以AB=AC=BC,△BAC是等边三角形,②正确;易知DA=DB=DC,又由②知③正确;由①知④错.
故选B.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
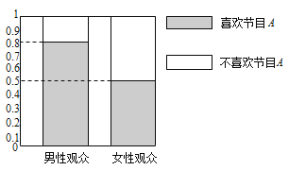
(1)根据该等高条形图,完成右上![]() 列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?
(2)从男性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附: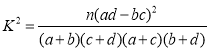
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |