题目内容
【题目】如图,三棱柱![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
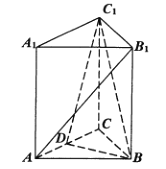
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值;
的余弦值;
(3)若点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,确定点
,确定点![]() 的位置并求线段
的位置并求线段![]() 的长。
的长。
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,求得
的中点,求得![]() ∥
∥![]() ,利用线面平行的判定定理,即可得到
,利用线面平行的判定定理,即可得到![]() ∥平面
∥平面![]() .
.
(2)以![]() 为原点,分别以
为原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系,求得平面
轴的正方向建立空间直角坐标系,求得平面![]() H和平面
H和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
(3)设![]() ,根据
,根据![]() 平面
平面![]() ,列出方程组,即可求解.
,列出方程组,即可求解.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,则点
,则点![]() 为
为![]() 的中点,
的中点,
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ∥
∥![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(2)因为![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]()
故以![]() 为原点,分别以
为原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向
轴的正方向
建立空间直角坐标系,
则![]() ,
,
所以![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则有 即
即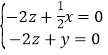
令![]() ,则得
,则得![]() .
.
又平面![]() 的法向量为
的法向量为![]() ,且二面角
,且二面角![]() 为锐角,
为锐角,
故二面角![]() 的余弦值为
的余弦值为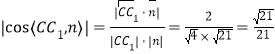
(3)设![]() 因为
因为![]() ,所以
,所以![]() ,
,
![]() .
.
又![]()
![]() ,
,![]() ,平面
,平面![]() ,
,
所以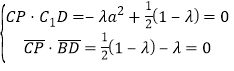 解得
解得![]()
所以![]() ,且点
,且点![]() 在线段
在线段![]() 的三等分点处,即
的三等分点处,即![]()

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
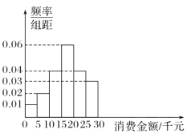
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
