题目内容
14．设随机变量X服从正态分布N（0，1），若P（x＞1）=0.4，则P（-1＜x＜0）=0.1．分析 画出正态分布N（0，1）的密度函数的图象，由图象的对称性可得结果．
解答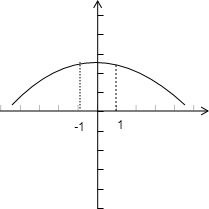 
解：画出正态分布N（0，1）的密度函数的图象如下图：
由图象的对称性可得，若P（ξ＞1）=0.4，则P（ξ＜-1）=0.4，
∴则P（-1＜ξ＜1）=1-2×0.4=0.2，
P（-1＜ξ＜0）=0.1．
故答案为：0.1
点评 本题考查正态分布，学习正态分布时需注意：从形态上看，正态分布是一条单峰、对称呈钟形的曲线，其对称轴为x=μ，并在x=μ时取最大值 从x=μ点开始，曲线向正负两个方向递减延伸，不断逼近x轴，但永不与x轴相交，因此说曲线在正负两个方向都是以x轴为渐近线的．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
2．若$\overrightarrow{m}$∥$\overrightarrow{n}$，$\overrightarrow{n}$∥$\overrightarrow{k}$，则向量$\overrightarrow{m}$与向量$\overrightarrow{k}$（ ）
| A． | 共线 | B． | 不共线 | C． | 共线且同向 | D． | 不一定共线 |
9．为了得到函数y=sin（2x+$\frac{π}{4}$）的图象，只需将函数y=cos（2x+$\frac{π}{3}$）的图象（ ）
| A． | 向左平移$\frac{7}{24}$π个单位 | B． | 向左平移$\frac{7}{12}$π个单位 | ||
| C． | 向右平移$\frac{7}{24}$π个单位 | D． | 向右平移$\frac{7}{12}$π个单位 |
已知抛物线M：y2=2px（p＞0），其焦点F到直线l：x-y-2t=0的距离为$\frac{3\sqrt{2}}{2}$．