题目内容
【题目】在直角坐标系xoy中,直线l经过点P(﹣1,0),其倾斜角为α,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0. (Ⅰ)若直线l与曲线C有公共点,求α的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求x+y的取值范围.
【答案】解:(Ⅰ)∵曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0,∴曲线C的直角坐标方程为x2+y2﹣6x+1=0 ∵直线l经过点P(﹣1,0),其倾斜角为α,∴直线l的参数方程为 ![]() (t为参数)
(t为参数)
将 ![]() ,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
∵直线l与曲线C有公共点,∴△=64cos2α﹣32≥0即 ![]() 或
或 ![]()
∵α∈[0,π)∴α的取值范围是 ![]()
(Ⅱ)曲线C的直角坐标方程为x2+y2﹣6x+1=0可化为(x﹣3)2+y2=8
其参数方程为 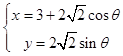 (θ为参数)
(θ为参数)
∵M(x,y)为曲线C上任意一点,∴ ![]()
∴x+y的取值范围是[﹣1,7].
【解析】(Ⅰ)由直线l经过点P(﹣1,0),且倾斜角为α,可得直线l的参数方程,利用互化公式可得C的直角坐标方程.由直线l与曲线C有公共点,可得△=64cos2α﹣32≥0,解出即可得出的取值范围; (Ⅱ)设M(x,y)为曲线C上任意一点,利用参数方程为 ![]() (θ为参数),结合三角函数知识求x+y的取值范围.
(θ为参数),结合三角函数知识求x+y的取值范围.

练习册系列答案
相关题目
