题目内容
【题目】设数列{an}首项a1=2,前n项和为Sn , 且满足2an+1+Sn=3(n∈N*),则满足 ![]() <
< ![]() <
< ![]() 的所有n的和为 .
的所有n的和为 .
【答案】9
【解析】解:由2an+1+Sn=3(n∈N*),
∴2an+2+Sn+1=3,
两式相减得2an+2+Sn+1﹣2an+1﹣Sn=0,
即2an+2+an+1﹣2an+1=0,
则2an+2=an+1 ,
当n=1时,2a2+a1=3,
则a2= ![]() ,满足2a2=a1 ,
,满足2a2=a1 ,
即2an+1=an , 则 ![]() =
= ![]() ,即数列{an}是公比q=
,即数列{an}是公比q= ![]() ,首项a1=2的等比数列,
,首项a1=2的等比数列,
则数列{an}前n项和为Sn= ![]() =4﹣4(
=4﹣4( ![]() )n ,
)n ,
∴ ![]() =
= 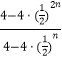 =1+(
=1+( ![]() )n ,
)n ,
∵ ![]() <
< ![]() <
< ![]() ,即
,即 ![]() <1+(
<1+( ![]() )n<
)n< ![]() ,
,![]() <(
<( ![]() )n<
)n< ![]() ,
,
则15<2n<33,
则n=4或5,
则4+5=9,
所以答案是:9.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系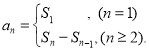 即可以解答此题.
即可以解答此题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目