题目内容
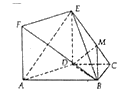
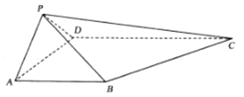
【题目】如图所示,在四棱锥![]() 中,
中, ![]() ,底面为梯形,
,底面为梯形, ![]() 且
且![]() 平面
平面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当异面直线![]() 与
与![]() 所成角为
所成角为![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)很明显![]() ,由线面垂直的定义可知
,由线面垂直的定义可知![]() ,则
,则![]() 平面
平面![]() ,结合面面垂直的判定定理可得平面
,结合面面垂直的判定定理可得平面![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由题意可得四边形
,由题意可得四边形![]() 为平行四边形,
为平行四边形, ![]() ,则
,则![]() ,结合(1)的结论有
,结合(1)的结论有![]() ,由几何关系可证得
,由几何关系可证得![]() 平面
平面![]() .据此由体积公式计算可得
.据此由体积公式计算可得![]() .
.
试题解析:
(1)![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
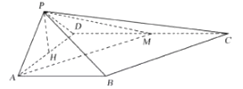
(2)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形, ![]() ,
,
则![]() 为异面直线
为异面直线![]() 所成的角,即
所成的角,即![]() ,
,
由(1)知, ![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
而![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
如图,取![]() 的中点
的中点![]() ,连接
,连接![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.

练习册系列答案
相关题目
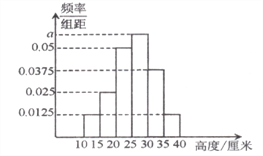
【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制.已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
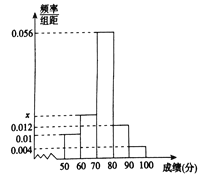
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高三学生中任选3人,求至少有1人成绩是及格以上等级的概率;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取3名学生进行学习经验介绍,记![]() 表示抽取的3名学生中优秀等级的学生人数,求随机变量
表示抽取的3名学生中优秀等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.