题目内容
1.数列{an}满足:a1=1,且对每个n∈N*,an,an+1是方程x2+3nx+bn=0的两根,则bn的前6项的和的4倍为( )| A. | 183 | B. | 132 | C. | 528 | D. | 732 |
分析 通过韦达定理可知an+an+1=-3n、an•an+1=bn,进而可知an+2-an=-3,通过n=1可知a2=-4,进而计算可得结论.
解答 解:∵an、an+1是方程x2+3nx+bn=0的两根,
∴an+an+1=-3n、an•an+1=bn,
∴an+2-an=-3,
∴a1,a3,a5,…和 a2,a4,a6…都是公差为-3的等差数列,
∴奇数项构成的数列为:{1,-2,-5,…},
偶数项构成的数列为:{-4,-7,-10,…},
∴b1+b2+b3+b4+b5+b6
=1×(-4)+(-4)×(-2)+(-2)×(-7)+(-7)×(-5)+(-5)×(-10)+(-10)×(-8)
=-4+8+14+35+50+80
=183,
∴4(b1+b2+b3+b4+b5+b6)=4×183=732,
故选:D.
点评 本题考查数列的通项,考查运算求解能力,分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.2015年安徽省文科高考数学试题考生一致认为比较简单,从而好成绩的取得不仅与知识掌握程度有关更与细节的把握程度有关(非知识错误)!学校就数学学科考试上是否有失误从本届文科毕业生中随机调查了100人,其中男生36人,有失误的学生中男生14人,女生16人.
(1)问:你有多大的把握认为细节的把握程度与性别有关?
(2)为了进一步调查考试中易犯哪些非知识错误,现用分层抽样的方法从100人中抽取样本容量为10的样本,求从这10人中任取两人,恰有一人犯有非知识错误的概率.
附:(1)临界值表:
(2)K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)问:你有多大的把握认为细节的把握程度与性别有关?
(2)为了进一步调查考试中易犯哪些非知识错误,现用分层抽样的方法从100人中抽取样本容量为10的样本,求从这10人中任取两人,恰有一人犯有非知识错误的概率.
附:(1)临界值表:
| p(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.已知集合A={x|(x+1)(4-x)<0},集合B={y|y=2sin3x},则A∩B=( )
| A. | (-1,2] | B. | ( 2,4 ) | C. | [-2,-1 ) | D. | [-2,2] |
11.函数f(x)=$\sqrt{1-2cos(2x-\frac{π}{3})}$的单调增区间为( )
| A. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ | B. | [kπ-$\frac{π}{3}$,kπ](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{2π}{3}$](k∈Z) |
 在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0.
在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0.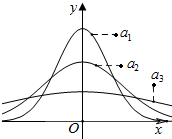 如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.
如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3. 如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.
如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.