题目内容
【题目】已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,其内接正方形的面积为4.
,其内接正方形的面积为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设M为椭圆C的右顶点,过点![]() 且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
【答案】(Ⅰ)![]() +
+![]() =1(Ⅱ)见解析
=1(Ⅱ)见解析
【解析】
(Ⅰ)由椭圆的离心率可以得到![]() 的关系,结合
的关系,结合![]() ,可知
,可知![]() 的关系,
的关系,
由对称性可得,可求椭圆内接正方形位于第一象限顶点的坐标,代入椭圆方程中,求出![]() 的值。
的值。
(Ⅱ)设了直线方程,与椭圆方程联立,得到一个一元二次方程,求出k1k2的表达式,利用一元二次方程根与系数的关系,对表达式进行化简求值。
解:(Ⅰ)∵e=![]() =
=![]() ,
,
∴a=![]() c,即a2=2b2,①,
c,即a2=2b2,①,
由对称性可得,椭圆内接正方形位于第一象限顶点的坐标为(x0,y0),
∴4x02=4,x0=1,
∴![]() +
+![]() =1,②,
=1,②,
由①②解得a=![]() ,b=
,b=![]() ,
,
∴椭圆C的标准方程为![]() +
+![]() =1.
=1.
(Ⅱ)由(Ⅰ)可知M(![]() ,0),依题意得直线l的斜率存在,设其方程为y=k(x-3
,0),依题意得直线l的斜率存在,设其方程为y=k(x-3![]() ),
),
设P(x1,y1),Q(x2,y2),(x1,x2≠![]() ),联立方程
),联立方程![]() ,消去y并整理可得
,消去y并整理可得
![]() ∴x1+x2=
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴k1k2=![]()
![]() =
=![]()
![]() =
=![]() =
=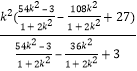 =
=![]() =1,
=1,
∴k1k2=1

练习册系列答案
相关题目