题目内容
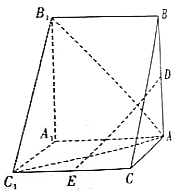
【题目】在三棱锥![]() 中,
中,![]() 是正三角形,面
是正三角形,面![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,由等腰三角形三线合一的性质得出
,由等腰三角形三线合一的性质得出![]() 且
且![]() ,利用直线与平面垂直的判定定理可证明出
,利用直线与平面垂直的判定定理可证明出![]() 面
面![]() ,从而得出
,从而得出![]() ;
;
(2)利用面面垂直的性质定理证明出![]() 平面
平面![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,然后利用空间向量法计算出二面角
轴建立空间直角坐标系,然后利用空间向量法计算出二面角![]() 的余弦值.
的余弦值.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() 且
且![]() .
.
又![]() ,
,![]() 面
面![]() ,又
,又![]() 面
面![]() ,
,![]() ;
;
(2)由面![]() 面
面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() 面
面![]() .
.
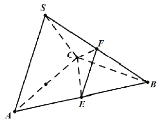
故以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,
轴,
建立如图所示空间直角坐标系:则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
![]() ,
,![]() ,设
,设![]() 为平面EFC的一个法向量
为平面EFC的一个法向量
由 ,取
,取![]() ,则
,则![]() ,
,![]() .
. ![]() .
.
又![]() 为面
为面![]() 的一个法向量,由
的一个法向量,由![]()
如图知二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天练口算系列答案
天天练口算系列答案【题目】为有效促进我市体育产业和旅游产业有机融合,提高我市的知名度,更好地宣传萍乡武功山,并通过赛事向社会各界传播健康、低碳、绿色、环保的运动理念。在今年9月21日第九届环鄱阳湖国际自行车大赛第九站比赛在我市武功山举行。在这次89.5公里的自行车个人赛中,其中25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:
14 | 0 | 1 | 2 | 3 | 5 | 6 | 6 | 6 | 6 | 8 | 9 |
15 | 0 | 2 | 3 | 4 | 5 | 5 | 5 | 7 | 9 | ||
16 | 0 | 0 | 5 | 6 | 7 |
男性 | 女性 | |
选择方案一 | 150 | 80 |
选择方案二 | 150 | 120 |
(1)是否有95%的把握认为方案的选择与性别有关?
(2)小明回答每道单选题的正确率为0.8,多选题的正确率为0.75,.
①若小明选择方案一,记小明的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
②如果你是小明,你觉得选择哪种方案更有可能获得赠品,请通过计算说明理由.
附:![]() ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |