题目内容
【题目】某中学为了组建一支业余足球队，在高一年级随机选取50名男生测量身高，发现被测男生的身高全部在
到
之间，将测量结果按如下方式分成六组：第1组
，第2组
，…，第6组
，如图是按上述分组得到的频率分布直方图，以频率近似概率.
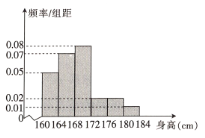
（1）若学校要从中选1名男生担任足球队长，求被选取的男生恰好在第5组或第6组的概率；
（2）试估计该校高一年级全体男生身高的平均数（同一组中的数据用该组区间的中点值代表）与中位数；
（3）现在从第5与第6组男生中选取两名同学担任守门员，求选取的两人中最多有1名男生来自第5组的概率.
【答案】（1）0.12；（2）平均数为168.72，中位数为168.25；（3）
.
【解析】
（1）由直方图可得，被选取的男生恰好在第5组或第6组的概率
；（2）每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值；直方图左右两边面积相等处横坐标表示中位数；（3）利用列举法，从第5与第6组男生中选取两名同学担任守门员共有15种情况，其中选取的两人中最多有1名男生来自第5组的情况有9种，由古典概型概率公式可得结果.
（1）被选取的男生恰好在第5组或第6组的概率
.
（2）全体男生身高的平均数为
.
设全体男生身高的中位数为
，因为第1组
对应的频率为0.20，第2组
对应的频率为0.28，所以
，则
，解得
.
（3）第5组有
人，记为
，
，
，
，同理第6组有2人记为
，
，
所有的情况为
、
、
、
、
、
、
、
、
、
、
、
、
、
、
，共15种，
选取的两人中最多有1名男生来自第5组的有、、、、、、、、共9种，
所以所求概率为
.
练习册系列答案
相关题目
