题目内容
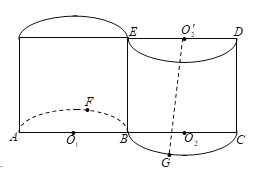
【题目】如图，两铁路线垂直相交于站
，若已知
千米，甲火车从站出发，沿
方向以
千米
小时的速度行驶，同时乙火车从
站出发，沿
方向，以
千米小时的速度行驶，至站即停止前行（甲车扔继续行驶）（两车的车长忽略不计）.
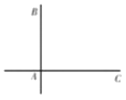
（1）求甲、乙两车的最近距离（用含的式子表示）；
（2）若甲、乙两车开始行驶到甲，乙两车相距最近时所用时间为
小时，问为何值时最大？
【答案】（1）
；（2）
时，
最大.
【解析】
（1）先设行驶
小时后，甲乙两车的距离最近，记此时甲车行驶到点
，乙车行驶到点
，根据题意，得到
，
，由勾股定理，表示出
，再由配方法，即可得出结果；
（2）先由（1）得
，根据基本不等式，即可得出结果.
（1）设行驶小时后，甲乙两车的距离最近，记此时甲车行驶到点，乙车行驶到点，
则，，
则
，
，
因为
，所以当
时，取到最小值，
即
取到最小值，此时
海里；
所以甲、乙两车的最近距离为；
（2）由（1）知，当甲、乙两车开始行驶到甲，乙两车相距最近时所用时间为
，
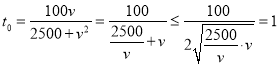当且仅当
，即时，最大.
世纪百通期末金卷系列答案
【题目】某超市开展年终大回馈，设计了两种答题游戏方案：
方案一：顾客先回答一道多选题，从第二道开始都回答单选题；
方案二：顾客全部选择单选题进行回答；
其中每道单选题答对得2分，每道多选题答对得3分，无论单选题还是多选题答错都得0分，每名参与的顾客至多答题3道.在答题过程中得到3分或3分以上立刻停止答题，并获得超市回馈的赠品.
为了调查顾客对方案的选择情况，研究人员调查了参与游戏的500名顾客，所得结果如下表所示：
男性 | 女性 | |
选择方案一 | 150 | 80 |
选择方案二 | 150 | 120 |
（1）是否有95%的把握认为方案的选择与性别有关？
（2）小明回答每道单选题的正确率为0.8，多选题的正确率为0.75,.
①若小明选择方案一，记小明的得分为
，求的分布列及期望；
②如果你是小明，你觉得选择哪种方案更有可能获得赠品，请通过计算说明理由.
附：
，
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
