题目内容
8.记函数f(n)=1+$\frac{x}{1!}$+$\frac{{x}^{2}}{2!}$+…+$\frac{{x}^{n}}{n!}$(n∈N+),求证:当n为偶数时,方程fn(x)=0没有实数根;当n为奇数时,方程fn(x)=0有唯一实数根xn,且xn+2<xn.分析 构造辅助函数Fn(x)=e-xfn(x)=e-x(1+$\frac{x}{1!}$+$\frac{{x}^{2}}{2!}$+…+$\frac{{x}^{n}}{n!}$).当n为偶数时求导得到
Fn′(x)=-e-x•$\frac{1}{(2k-1)!}{x}^{2k-1}$,从而得到Fn(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.
求得Fn(x)max=Fn(0)=0后说明n为偶数时,Fn(x)=0无解,从而方程fn(x)=0没有实数根;当n为奇数时,设Fn(x)=e-xfn(x)=e-x(1+$\frac{x}{1!}$+$\frac{{x}^{2}}{2!}$+…+$\frac{{x}^{n}}{n!}$).由其导数小于0说明y=Fn(x)为R上的减函数,而
F(1)>0,F(-1)<0,说明Fn(x)=0有唯一解,从而方程fn(x)=0有唯一实数根xn,且xn+2<xn.
解答 证明:当n为偶数时,设Fn(x)=e-xfn(x)=e-x(1+$\frac{x}{1!}$+$\frac{{x}^{2}}{2!}$+…+$\frac{{x}^{n}}{n!}$).
设n=2k(k∈N+),则Fn′(x)=-e-x•$\frac{1}{(2k-1)!}{x}^{2k-1}$,
当x<0时,Fn′(x)>0,当x>0时,Fn′(x)<0,
∴Fn(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.
∴Fn(x)max=Fn(0)=0,
∴n为偶数时,Fn(x)=0无解,从而方程fn(x)=0没有实数根;
当n为奇数时,设Fn(x)=e-xfn(x)=e-x(1+$\frac{x}{1!}$+$\frac{{x}^{2}}{2!}$+…+$\frac{{x}^{n}}{n!}$).
设n=2k+1(k∈N+),则Fn′(x)=-e-x•$\frac{1}{(2k)!}{x}^{2k}$<0,
∴y=Fn(x)为R上的减函数,而F(1)>0,F(-1)<0,
∴Fn(x)=0有唯一解,从而方程fn(x)=0有唯一实数根xn,且xn+2<xn.
点评 考查函数的单调性,考查函数的最值,解题的关键是构造新函数且应用函数的导函数求解,注意函数和方程之间的关系,是有一定难度题目.

 名师点拨卷系列答案
名师点拨卷系列答案| A. | 128 | B. | -128 | C. | 64 | D. | -64 |
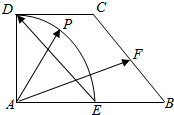 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].