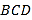题目内容
【题目】已知椭圆![]()
![]() 的焦点坐标分別为
的焦点坐标分別为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,满足
上一点,满足![]() 且
且![]()
(1) 求椭圆![]() 的标准方程:
的标准方程:
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:第一问首先根据题中条件将涉及到的量设出来,之后结合椭圆的定义以及对应的线段的倍数关系,求得对应的边长,利用余弦定理借用余弦值建立边之间的等量关系式,从而求得![]() 的值,借用椭圆中
的值,借用椭圆中![]() 的关系,求得b的值,从而求得椭圆的方程,第二问将直线的方程与椭圆的方程联立,求得两根和与两根积,从而求得线段的中点,利用条件可得垂直关系,建立等量关系式,借用判别式大于零找到其所满足的不等关系,求得k的取值范围.
的关系,求得b的值,从而求得椭圆的方程,第二问将直线的方程与椭圆的方程联立,求得两根和与两根积,从而求得线段的中点,利用条件可得垂直关系,建立等量关系式,借用判别式大于零找到其所满足的不等关系,求得k的取值范围.
详解:(1)由题意设![]() ,
,![]() 则
则![]() ,又
,又![]() ,
,![]() ,
,![]()
在 ![]() 中,由余弦定理得,
中,由余弦定理得,![]()
![]()
![]()
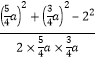
![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,![]() 所求椭圆方程为
所求椭圆方程为![]()
(2)联立方程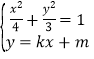 ,消去
,消去![]() 得
得![]()
![]() ,
,
则![]()
![]() ,
,![]() ,且
,且![]() …①
…①
设![]() 的中心为
的中心为![]() ,则
,则![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,即,
,即,![]()
 ,解得
,解得![]() …②
…②
把②代入①得![]() ,整理得
,整理得![]() ,即
,即![]()
解得![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
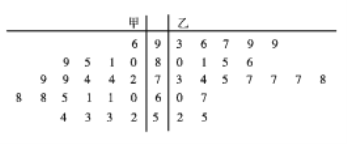
【题目】为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.
(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)