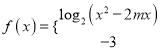题目内容
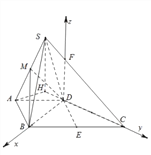
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为钝角三角形且垂直于底面
为钝角三角形且垂直于底面![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与底面
与底面![]() 所成的角为60°,求二面角
所成的角为60°,求二面角![]() 余弦值.
余弦值.

【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,由勾股定理可得
,由勾股定理可得![]() ,结合面面垂直的性质定理可得证;
,结合面面垂直的性质定理可得证;
(Ⅱ)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,可证得
,可证得![]() 为斜线
为斜线![]() 与底面
与底面![]() 所成的角,进而得
所成的角,进而得![]() ,过点
,过点![]() 作
作![]() ,所以
,所以![]() 底面
底面![]() ,所以
,所以![]() 两两垂直,建立空间直角坐标系,利用空间向量求解二面角即可.
两两垂直,建立空间直角坐标系,利用空间向量求解二面角即可.
详解:
(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,
,
依题意得,四边形![]() 为正方形,且有
为正方形,且有![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(Ⅱ)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,
,
因为平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,
,![]()
![]() 平面
平面![]() ,所以
,所以![]() 底面
底面![]() ,故
,故![]() 为斜线
为斜线![]() 在底面
在底面![]() 内的射影,
内的射影,
![]() 为斜线
为斜线![]() 与底面
与底面![]() 所成的角,即
所成的角,即![]()
由(Ⅰ)得,![]() ,所以在
,所以在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
所以![]() ,从而
,从而![]() ,
,
过点![]() 作
作![]() ,所以
,所以![]() 底面
底面![]() ,
,
所以![]() 两两垂直,如图,以点
两两垂直,如图,以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]()
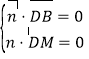 得
得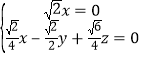
取![]() 得
得![]() ,
,
设平面![]() 的法向量
的法向量![]()
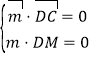 得
得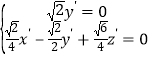 ,
,
取![]() 得,
得,![]() ,
,
所以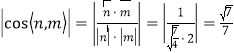
故所求的二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.
【题目】2018年3月3日至20日中华人民共和国第十三届全国人民代表大会第一次会议和中国人民政治协商会议第十三届全国委员会第一次会议在北京胜利召开,两会是年度中国政治生活中的一件大事,受到了举国上下和全世界的广泛关注.为及时宣传国家政策,贯彻两会精神,某校举行了全国两会知识竞赛,为了解本次竞赛成绩情况,随机抽取了部分学生的成绩(得分均为整数,满分![]() 分,最低分不低于
分,最低分不低于![]() 分)进行统计,得出频率分布表如下:
分)进行统计,得出频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)求表中![]() 、
、![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从成绩较好的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人担任两会知识宣传员,再从这
人担任两会知识宣传员,再从这![]() 人中随机选出
人中随机选出![]() 人负责整理两会相关材料,求这
人负责整理两会相关材料,求这![]() 人中至少有
人中至少有![]() 人来自第
人来自第![]() 组的概率.
组的概率.