题目内容
19. 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为(x-1)2+(y-$\sqrt{2}$)2=2;
(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:
①$\frac{|NA|}{|NB|}$=$\frac{|MA|}{|MB|}$; ②$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2; ③$\frac{|NB|}{|NA|}$+$\frac{|MA|}{|MB|}$=2$\sqrt{2}$.
其中正确结论的序号是①②③.(写出所有正确结论的序号)
分析 (1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;
(2)设M(cosα,sinα),N(cosβ,sinβ),计算出$\frac{|MA|}{|MB|}$、$\frac{|NA|}{|NB|}$、$\frac{|NB|}{|NA|}$的值即可.
解答 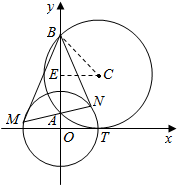 解:(1)∵圆C与x轴相切于点T(1,0),
解:(1)∵圆C与x轴相切于点T(1,0),
∴圆心的横坐标x=1,取AB的中点E,
∵|AB|=2,∴|BE|=1,
则|BC|=$\sqrt{2}$,即圆的半径r=|BC|=$\sqrt{2}$,
∴圆心C(1,$\sqrt{2}$),
则圆的标准方程为(x-1)2+(y-$\sqrt{2}$)2=2,
故答案为:(x-1)2+(y-$\sqrt{2}$)2=2.
(2)∵圆心C(1,$\sqrt{2}$),∴E(0,$\sqrt{2}$),
又∵|AB|=2,且E为AB中点,
∴A(0,$\sqrt{2}$-1),B(0,$\sqrt{2}$+1),
∵M、N在圆O:x2+y2=1上,
∴可设M(cosα,sinα),N(cosβ,sinβ),
∴|NA|=$\sqrt{(cosβ-0)^{2}+[sinβ-(\sqrt{2}-1{)]}^{2}}$
=$\sqrt{co{s}^{2}β+si{n}^{2}β-2(\sqrt{2}-1)sinβ+3-2\sqrt{2}}$
=$\sqrt{4-2\sqrt{2}-2(\sqrt{2}-1)sinβ}$
=$\sqrt{2\sqrt{2}(\sqrt{2}-1)-2(\sqrt{2}-1)sinβ}$
=$\sqrt{2(\sqrt{2}-1)(\sqrt{2}-sinβ)}$,
|NB|=$\sqrt{(cosβ-0)^{2}+[sinβ-(\sqrt{2}+1)]^{2}}$
=$\sqrt{co{s}^{2}β+si{n}^{2}β-2(\sqrt{2}+1)sinβ+3+2\sqrt{2}}$
=$\sqrt{4+2\sqrt{2}-2(\sqrt{2}+1)sinβ}$
=$\sqrt{2(\sqrt{2}+1)(\sqrt{2}-sinβ)}$,
∴$\frac{|NA|}{|NB|}$=$\sqrt{\frac{2(\sqrt{2}-1)(\sqrt{2}-sinβ)}{2(\sqrt{2}+1)(\sqrt{2}-sinβ)}}$=$\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}$=$\sqrt{2}-1$,
同理可得$\frac{|MA|}{|MB|}$=$\sqrt{2}-1$,
∴$\frac{|NA|}{|NB|}$=$\frac{|MA|}{|MB|}$,①成立,
$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=$\frac{1}{\sqrt{2}-1}$-($\sqrt{2}-1$)=2,②正确.
$\frac{|NB|}{|NA|}$+$\frac{|MA|}{|MB|}$=$\frac{1}{\sqrt{2}-1}$+($\sqrt{2}-1$)=$2\sqrt{2}$,③正确.
故答案为:①②③.
点评 本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.求直线D1E与平面A1D1B所成角的正弦值.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.求直线D1E与平面A1D1B所成角的正弦值.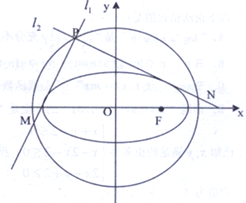 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$