题目内容
7．已知函数f（x）=x3-kx2+x（x∈R），当k=1时，f（x）的单调区间为单调增区间：R．分析 先确定函数的定义域然后求导数fˊ（x），在函数的定义域内解不等式f′（x）＞0和f′（x）＜0．
解答 解：函数f（x）=x3-kx2+x（x∈R），当k=1时，f（x）=x3-x2+x，
f′（x）=3x2-2x+1，
由f′（x）＞0，得x∈R，
故函数的单调递增区间为：（-∞，+∞）；
由f'（x）＜0得x∈∅．
故答案为：单调增区间：R．
点评 本题主要考查利用导数判断函数的单调性的步骤：（1）确定 的定义域；（2）求导数fˊ（x）；（3）在函数 的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0（4）确定 的单调区间．若在函数式中含字母系数，往往要分类讨论．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
17．如图是一个几何体的三视图，则该几何体可能是（ ）
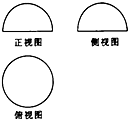
| A． | 半球 | B． | 球 | C． | 圆柱 | D． | 圆锥 |
18．下列说法中正确的是（ ）
| A． | 命题“若a＞b＞0，则$\frac{1}{a}＜\frac{1}{b}$”的逆命题是真命题 | |
| B． | 命题p：?x∈R，2x＞0，则￢p：?x0∈R，2x0＜0 | |
| C． | “a＞1，b＞1”是“ab＞1”成立的充分条件 | |
| D． | “a＞b”是“a2＞b2”成立的充分不必要条件 |
15．偶函数f（x）=loga|x+b|在（-∞，0）上单调递减，则f（a+1）与f（2-b）的大小关系是（ ）
| A． | f（a+1）＞f（2-b） | B． | f（a+1）=f（2-b） | C． | f（a+1）＜f（2-b） | D． | 不能确定 |
如图：四棱锥P-ABCD中，底面ABCD是边长为2的正方形，平面PCD⊥底面ABCD，且PC=PD=a．
如图，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．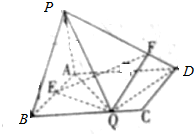
如图所示，在矩形ABCD中，AB=1，AD=a，PA⊥平面ABCD，且PA=1，E为AB中点，F、Q分别在边PD、BC上，$\overrightarrow{PF}$=λ$\overrightarrow{PD}$，λ∈（0，1），且仅存在唯一一点Q，使得PQ⊥QD．